Question Number 92041 by mhmd last updated on 04/May/20
![solve :[ 2yy′′=1+(y′)^2 ] if y(0)=2 , y′(0)=−1](https://www.tinkutara.com/question/Q92041.png)
$${solve}\::\left[\:\:\mathrm{2}{yy}''=\mathrm{1}+\left({y}'\right)^{\mathrm{2}} \:\right]\:{if}\:{y}\left(\mathrm{0}\right)=\mathrm{2}\:,\:{y}'\left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$ \\ $$
Answered by mr W last updated on 04/May/20
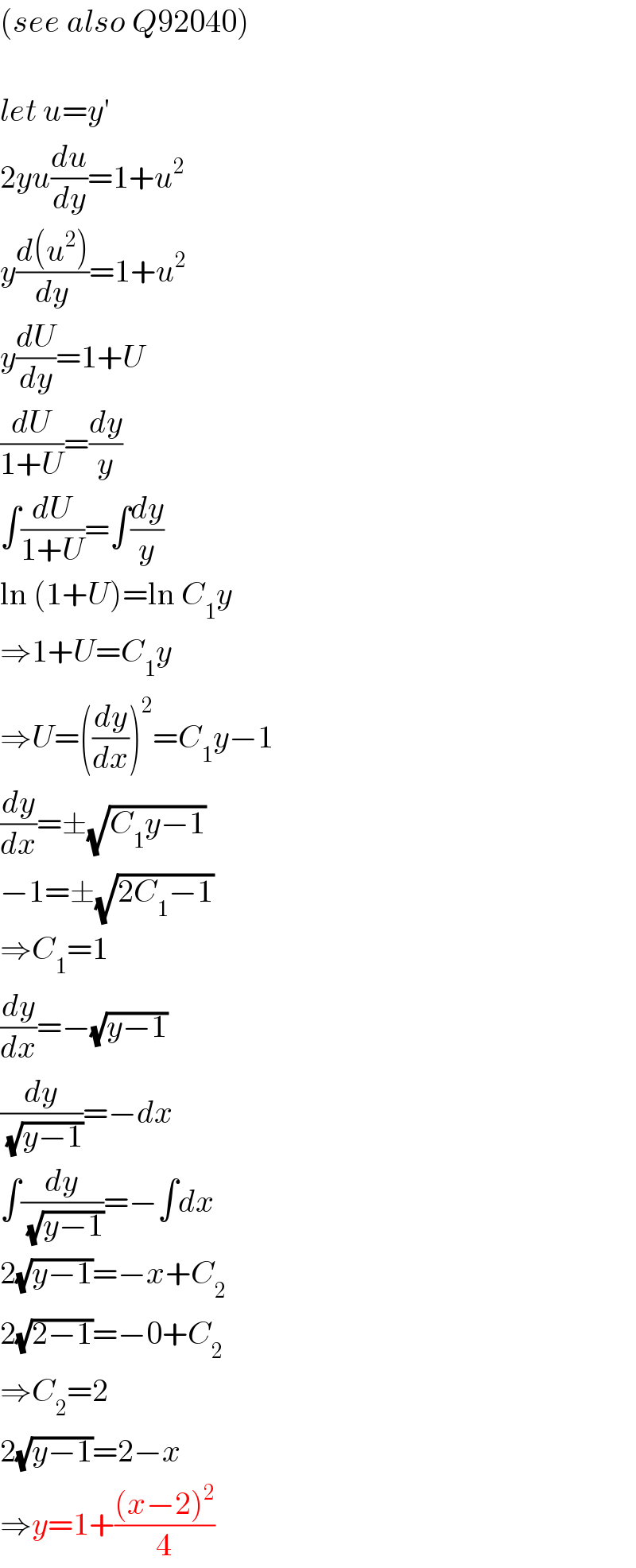
$$\left({see}\:{also}\:{Q}\mathrm{92040}\right) \\ $$$$ \\ $$$${let}\:{u}={y}' \\ $$$$\mathrm{2}{yu}\frac{{du}}{{dy}}=\mathrm{1}+{u}^{\mathrm{2}} \\ $$$${y}\frac{{d}\left({u}^{\mathrm{2}} \right)}{{dy}}=\mathrm{1}+{u}^{\mathrm{2}} \\ $$$${y}\frac{{dU}}{{dy}}=\mathrm{1}+{U} \\ $$$$\frac{{dU}}{\mathrm{1}+{U}}=\frac{{dy}}{{y}} \\ $$$$\int\frac{{dU}}{\mathrm{1}+{U}}=\int\frac{{dy}}{{y}} \\ $$$$\mathrm{ln}\:\left(\mathrm{1}+{U}\right)=\mathrm{ln}\:{C}_{\mathrm{1}} {y} \\ $$$$\Rightarrow\mathrm{1}+{U}={C}_{\mathrm{1}} {y} \\ $$$$\Rightarrow{U}=\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} ={C}_{\mathrm{1}} {y}−\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=\pm\sqrt{{C}_{\mathrm{1}} {y}−\mathrm{1}} \\ $$$$−\mathrm{1}=\pm\sqrt{\mathrm{2}{C}_{\mathrm{1}} −\mathrm{1}} \\ $$$$\Rightarrow{C}_{\mathrm{1}} =\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=−\sqrt{{y}−\mathrm{1}} \\ $$$$\frac{{dy}}{\:\sqrt{{y}−\mathrm{1}}}=−{dx} \\ $$$$\int\frac{{dy}}{\:\sqrt{{y}−\mathrm{1}}}=−\int{dx} \\ $$$$\mathrm{2}\sqrt{{y}−\mathrm{1}}=−{x}+{C}_{\mathrm{2}} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}−\mathrm{1}}=−\mathrm{0}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{C}_{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{2}\sqrt{{y}−\mathrm{1}}=\mathrm{2}−{x} \\ $$$$\Rightarrow{y}=\mathrm{1}+\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$
