Menu Close

solve-3-sin2x-2cos-2-x-3-1-sin2x-2sin-2-x-28-

Tinku Tara 0 Comments
Pin




Question Number 44920 by peter frank last updated on 06/Oct/18
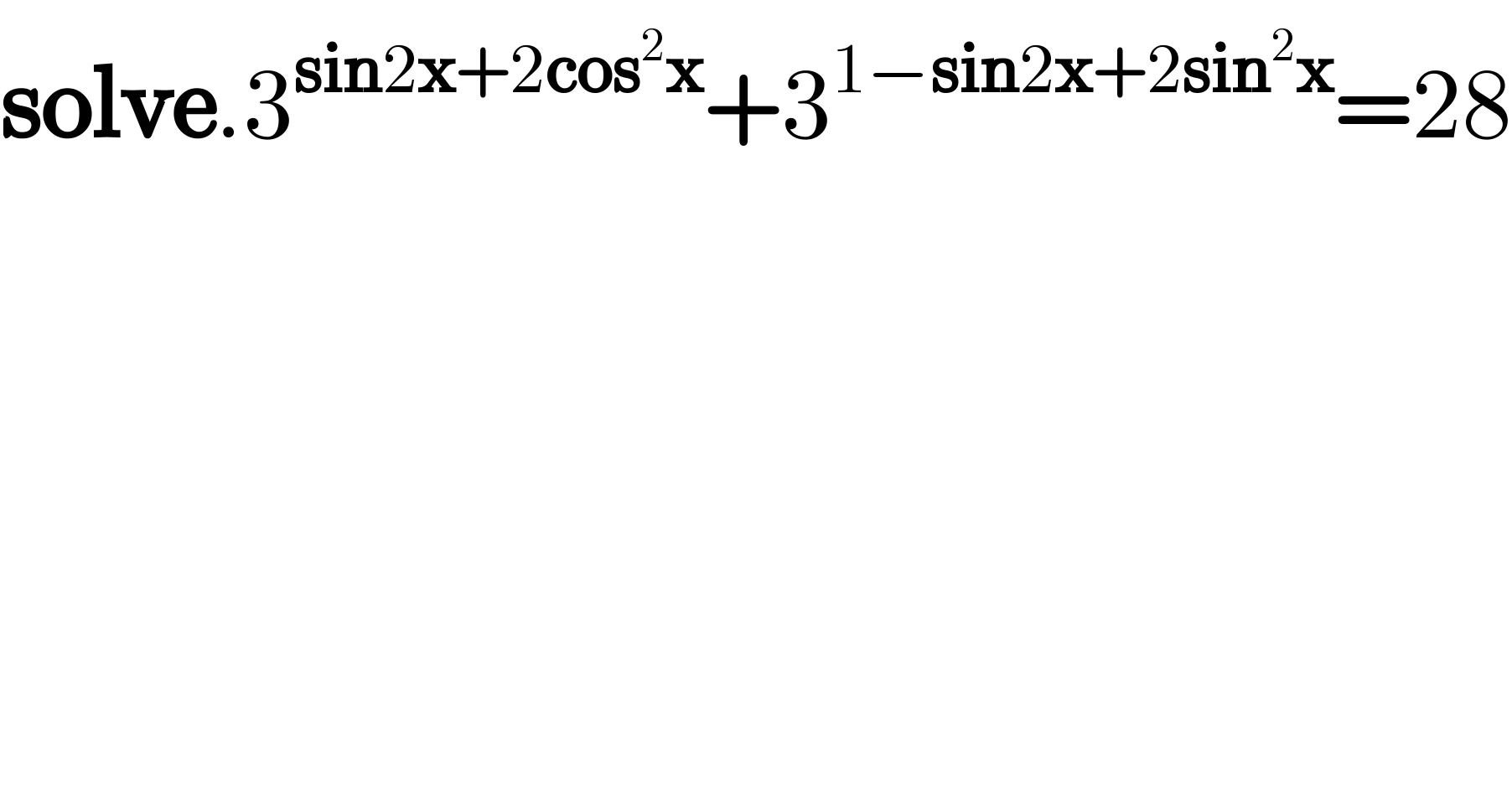
solve.3^(sin2x+2cos^2 x) +3^(1−sin2x+2sin^2 x) =28
$$\boldsymbol{\mathrm{solve}}.\mathrm{3}^{\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} +\mathrm{3}^{\mathrm{1}−\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{2}\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} =\mathrm{28} \\ $$
Answered by ajfour last updated on 06/Oct/18
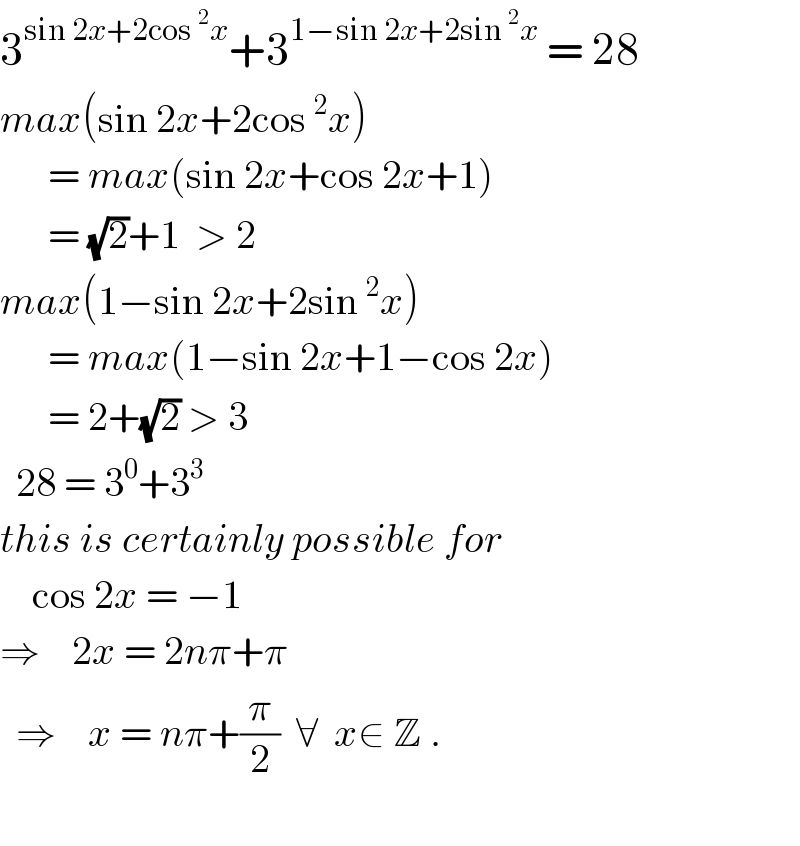
3^(sin 2x+2cos^2 x) +3^(1−sin 2x+2sin^2 x) = 28 max(sin 2x+2cos^2 x) = max(sin 2x+cos 2x+1) = (√2)+1 > 2 max(1−sin 2x+2sin^2 x) = max(1−sin 2x+1−cos 2x) = 2+(√2) > 3 28 = 3^0 +3^3 this is certainly possible for cos 2x = −1 ⇒ 2x = 2nπ+π ⇒ x = nπ+(π/2) ∀ x∈ Z .
$$\mathrm{3}^{\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2cos}\:^{\mathrm{2}} {x}} +\mathrm{3}^{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}} \:=\:\mathrm{28} \\ $$$${max}\left(\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2cos}\:^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:=\:{max}\left(\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:=\:\sqrt{\mathrm{2}}+\mathrm{1}\:\:>\:\mathrm{2} \\ $$$${max}\left(\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:=\:{max}\left(\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}+\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{2}+\sqrt{\mathrm{2}}\:>\:\mathrm{3} \\ $$$$\:\:\mathrm{28}\:=\:\mathrm{3}^{\mathrm{0}} +\mathrm{3}^{\mathrm{3}} \\ $$$${this}\:{is}\:{certainly}\:{possible}\:{for} \\ $$$$\:\:\:\:\mathrm{cos}\:\mathrm{2}{x}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}{x}\:=\:\mathrm{2}{n}\pi+\pi \\ $$$$\:\:\Rightarrow\:\:\:\:{x}\:=\:{n}\pi+\frac{\pi}{\mathrm{2}}\:\:\forall\:\:{x}\in\:\mathbb{Z}\:. \\ $$$$\:\:\: \\ $$
Answered by hknkrc46 last updated on 24/Dec/18
3^(sin 2x+2cos^2 x) +3^(1−sin 2x+2sin^2 x) =28 3^(sin 2x+(cos 2x+1)) +3^(1−sin 2x+(1−cos 2x)) 3^((sin 2x+cos 2x)+1) +3^(2−(sin 2x+cos 2x)) ⇒ sin 2x+cos 2x=−1 ⇒2sin xcos x+cos^2 x−sin^2 x=−cos^2 x−sin^2 x ⇒2cos^2 x+2sin xcos x=0 ⇒ cos x(cos x+sin x)=0 ⇒ cos x=0 ∨ cos x+sin x=0 ⇒ cos x=0 ∨ (cos x+sin x)^2 =0 ⇒ cos x=0 ∨ 1+sin 2x=0 ⇒ cos x=0 ∨ sin 2x=−1 ⇒x=(((4k+3)/4))π , k∈Z
$$\mathrm{3}^{\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2cos}\:^{\mathrm{2}} {x}} +\mathrm{3}^{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}} =\mathrm{28} \\ $$$$ \\ $$$$\mathrm{3}^{\mathrm{sin}\:\mathrm{2}{x}+\left(\mathrm{cos}\:\mathrm{2}{x}+\mathrm{1}\right)} +\mathrm{3}^{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}+\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)} \\ $$$$\mathrm{3}^{\left(\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}\right)+\mathrm{1}} +\mathrm{3}^{\mathrm{2}−\left(\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}\right)} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2sin}\:{x}\mathrm{cos}\:{x}+\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}=−\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\Rightarrow\mathrm{2cos}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}=\mathrm{0}\:\vee\:\mathrm{cos}\:{x}+\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}=\mathrm{0}\:\vee\:\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}=\mathrm{0}\:\vee\:\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}=\mathrm{0}\:\vee\:\mathrm{sin}\:\mathrm{2}{x}=−\mathrm{1} \\ $$$$\Rightarrow{x}=\left(\frac{\mathrm{4}{k}+\mathrm{3}}{\mathrm{4}}\right)\pi\:,\:{k}\in\mathbb{Z} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *