solve-3-x-3x-10-

Question Number 160235 by mr W last updated on 26/Nov/21

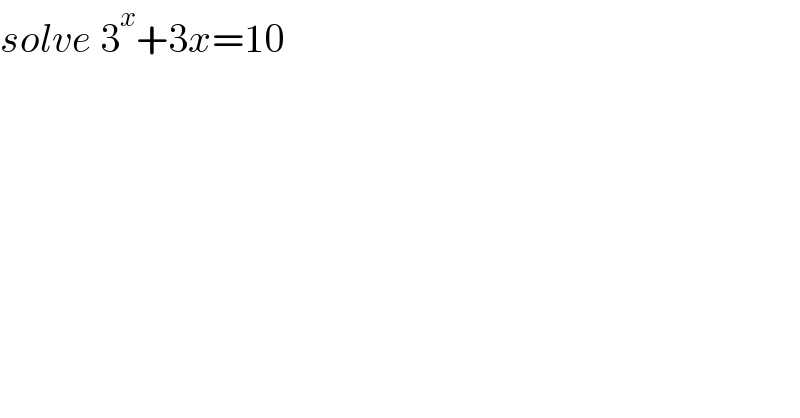
$${solve}\:\mathrm{3}^{{x}} +\mathrm{3}{x}=\mathrm{10} \\ $$

Answered by FongXD last updated on 26/Nov/21

⇔ e^(xln3) =10−3x ⇔ (10−3x)e^(−xln3) =1 mulitiply both sides by ((ln3)/3)e^((10ln3)/3) ⇔ (((10ln3)/3)−xln3)e^(((10ln3)/3)−xln3) =((ln3)/3)e^((10ln3)/3) ⇔ W((((10ln3)/3)−xln3)e^(((10ln3)/3)−xln3) )=W(((ln3)/3)e^((10ln3)/3) ) ⇔ ((10ln3)/3)−xln3=W(((ln3)/3)×3^((10)/3) ) ⇒ x=((10)/3)−((W(3^(7/3) ln3))/(ln3))

$$\Leftrightarrow\:\mathrm{e}^{\mathrm{xln3}} =\mathrm{10}−\mathrm{3x} \\ $$$$\Leftrightarrow\:\left(\mathrm{10}−\mathrm{3x}\right)\mathrm{e}^{−\mathrm{xln3}} =\mathrm{1} \\ $$$$\mathrm{mulitiply}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:\frac{\mathrm{ln3}}{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{10ln3}}{\mathrm{3}}} \\ $$$$\Leftrightarrow\:\left(\frac{\mathrm{10ln3}}{\mathrm{3}}−\mathrm{xln3}\right)\mathrm{e}^{\frac{\mathrm{10ln3}}{\mathrm{3}}−\mathrm{xln3}} =\frac{\mathrm{ln3}}{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{10ln3}}{\mathrm{3}}} \\ $$$$\Leftrightarrow\:\mathrm{W}\left(\left(\frac{\mathrm{10ln3}}{\mathrm{3}}−\mathrm{xln3}\right)\mathrm{e}^{\frac{\mathrm{10ln3}}{\mathrm{3}}−\mathrm{xln3}} \right)=\mathrm{W}\left(\frac{\mathrm{ln3}}{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{10ln3}}{\mathrm{3}}} \right) \\ $$$$\Leftrightarrow\:\frac{\mathrm{10ln3}}{\mathrm{3}}−\mathrm{xln3}=\mathrm{W}\left(\frac{\mathrm{ln3}}{\mathrm{3}}×\mathrm{3}^{\frac{\mathrm{10}}{\mathrm{3}}} \right) \\ $$$$\Rightarrow\:\mathrm{x}=\frac{\mathrm{10}}{\mathrm{3}}−\frac{\mathrm{W}\left(\mathrm{3}^{\frac{\mathrm{7}}{\mathrm{3}}} \mathrm{ln3}\right)}{\mathrm{ln3}} \\ $$

Commented by mr W last updated on 26/Nov/21

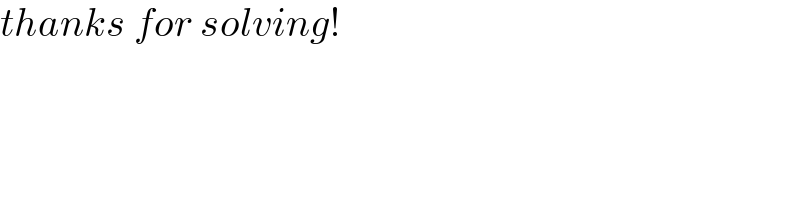
$${thanks}\:{for}\:{solving}! \\ $$

Commented by FongXD last updated on 26/Nov/21

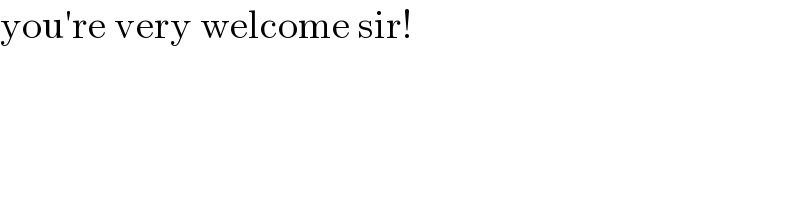
$$\mathrm{you}'\mathrm{re}\:\mathrm{very}\:\mathrm{welcome}\:\mathrm{sir}! \\ $$

Answered by MathsFan last updated on 26/Nov/21

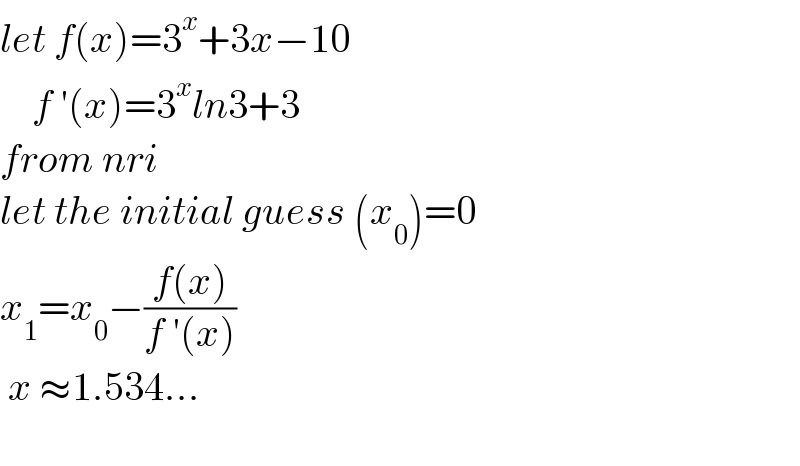
let f(x)=3^x +3x−10 f ′(x)=3^x ln3+3 from nri let the initial guess (x_0 )=0 x_1 =x_0 −((f(x))/(f ′(x))) x ≈1.534...

$${let}\:{f}\left({x}\right)=\mathrm{3}^{{x}} +\mathrm{3}{x}−\mathrm{10} \\ $$$$\:\:\:\:{f}\:'\left({x}\right)=\mathrm{3}^{{x}} {ln}\mathrm{3}+\mathrm{3} \\ $$$${from}\:{nri}\: \\ $$$${let}\:{the}\:{initial}\:{guess}\:\left({x}_{\mathrm{0}} \right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ={x}_{\mathrm{0}} −\frac{{f}\left({x}\right)}{{f}\:'\left({x}\right)} \\ $$$$\:{x}\:\approx\mathrm{1}.\mathrm{534}… \\ $$$$ \\ $$

Commented by mr W last updated on 26/Nov/21

$${thanks}\:{for}\:{trying}!\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply