Menu Close

Solve-39-10-a-a-2-9-a-2-2-14-a-R-Mr-Rasheed-yesterday-i-solved-it-on-a-draft-paper-When-i-came-today-to-write-it-down-on-the-notebook-i-got-into-a-maze-do-you

Tinku Tara 0 Comments
Pin




Question Number 182681 by Acem last updated on 12/Dec/22
Solve (√(39− 10 a −a^2 )) + (√(9−a^2 )) = 2 (√(14)) ; a∈ R^(+★) @Mr. Rasheed, yesterday i solved it on a draft paper When i came today to write it down on the notebook i got into a maze, do you have an easy way to deal with? “if you have time” i lost that paper, and this formula makes me laugh at myself, it′s for 13 y/o “confused face” Sure Every friend can share!
$$\:{Solve}\:\sqrt{\mathrm{39}−\:\mathrm{10}\:{a}\:−{a}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\:\mathrm{2}\:\sqrt{\mathrm{14}}\:\:\:;\:{a}\in\:\mathbb{R}^{+\bigstar} \\ $$$$\:@{Mr}.\:{Rasheed},\:{yesterday}\:{i}\:{solved}\:{it}\:{on}\:{a}\:{draft}\:{paper} \\ $$$$\:{When}\:{i}\:{came}\:{today}\:{to}\:{write}\:{it}\:{down}\:{on} \\ $$$$\:{the}\:{notebook}\:{i}\:{got}\:{into}\:{a}\:{maze},\:{do}\:{you}\:{have} \\ $$$$\:{an}\:{easy}\:{way}\:{to}\:{deal}\:{with}?\:“{if}\:{you}\:{have}\:{time}'' \\ $$$$\:{i}\:{lost}\:{that}\:{paper},\:{and}\:{this}\:{formula}\:{makes}\:{me} \\ $$$$\:{laugh}\:{at}\:{myself},\:{it}'{s}\:{for}\:\mathrm{13}\:{y}/{o}\:“{confused}\:{face}''\: \\ $$$$\:{Sure}\:{Every}\:{friend}\:{can}\:{share}! \\ $$
Commented by mr W last updated on 12/Dec/22
2(√(14)) or 2(√(24)) ?
$$\mathrm{2}\sqrt{\mathrm{14}}\:{or}\:\mathrm{2}\sqrt{\mathrm{24}}\:? \\ $$
Commented by Acem last updated on 12/Dec/22
No, it′s about 1.383 8 Sir , am not ok right now i will solve it again later though it′s so boring
$${No},\:{it}'{s}\:{about}\:\mathrm{1}.\mathrm{383}\:\mathrm{8}\:{Sir}\:,\:{am}\:{not}\:{ok}\:{right}\:{now} \\ $$$$\:{i}\:{will}\:{solve}\:{it}\:{again}\:{later}\:{though}\:{it}'{s}\:{so}\:{boring} \\ $$$$\: \\ $$
Commented by mr W last updated on 13/Dec/22
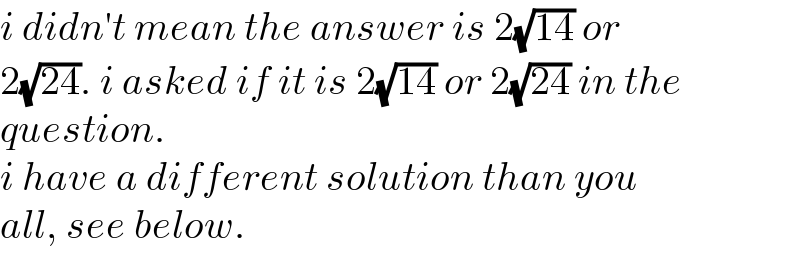
i didn′t mean the answer is 2(√(14)) or 2(√(24)). i asked if it is 2(√(14)) or 2(√(24)) in the question. i have a different solution than you all, see below.
$${i}\:{didn}'{t}\:{mean}\:{the}\:{answer}\:{is}\:\mathrm{2}\sqrt{\mathrm{14}}\:{or} \\ $$$$\mathrm{2}\sqrt{\mathrm{24}}.\:{i}\:{asked}\:{if}\:{it}\:{is}\:\mathrm{2}\sqrt{\mathrm{14}}\:{or}\:\mathrm{2}\sqrt{\mathrm{24}}\:{in}\:{the}\: \\ $$$${question}. \\ $$$${i}\:{have}\:{a}\:{different}\:{solution}\:{than}\:{you} \\ $$$${all},\:{see}\:{below}. \\ $$
Commented by manxsol last updated on 13/Dec/22
Sir W could share his solution.I would appreciate it if you critque my solution.
$$ \\ $$$$\mathrm{Sir}\:\mathrm{W}\:\mathrm{could}\:\mathrm{share}\:\mathrm{his}\:\mathrm{solution}.\mathrm{I} \\ $$$$\:\mathrm{would}\:\mathrm{appreciate}\:\mathrm{it}\:\mathrm{if}\:\mathrm{you} \\ $$$$\mathrm{critque}\:\mathrm{my}\:\mathrm{solution}. \\ $$
Commented by manxsol last updated on 14/Dec/22
combination metod friz+metod rasheed solution (√x)+(√y)=(√u) x(a),y(a), u=k 4ux=[u+(x−y)]^2 I 4uy=[u−(x−y)]^2 II sea x−y=qa+b lineal solve I ⇒ma^2 +na+p solve II⇒ ma^2 +na+p solve ma^2 +na+p=0 a_1 a_2 DEVELOPING (√x)+(√y)=(√u) ((√x)−(√y))((√x)+(√y))=(√u)((√x)−(√y)) x−y=(√u) ((√x)−(√y)) .................. (√x)−(√y)=(((x−y))/( (√u))) (√x)+(√y)=(√u) .................. add 2(√x)=(((u+(x−y)))/( (√u))) 4xu=(u+(x−y)^2 ) 4yu=(u−(x−y)^2 ) CONCLUSION (√x)+(√y)=(√u) is equivalent a solve {4xu=(u+(x−y))^2 } ∪ {4yu=(u−(x−y))^(2 ) }
$${combination}\: \\ $$$${metod}\:{friz}+{metod}\:{rasheed} \\ $$$${solution} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{{u}}\:\:\:\:\:\:\:{x}\left({a}\right),{y}\left({a}\right),\:{u}={k} \\ $$$$\mathrm{4}{ux}=\left[{u}+\left({x}−{y}\right)\right]^{\mathrm{2}} \:\:\:\:\:{I} \\ $$$$\mathrm{4}{uy}=\left[{u}−\left({x}−{y}\right)\right]^{\mathrm{2}} \:\:\:\:\:{II} \\ $$$${sea}\:\:{x}−{y}={qa}+{b}\:\:\:\:{lineal} \\ $$$${solve}\:{I}\:\:\:\Rightarrow{ma}^{\mathrm{2}} +{na}+{p} \\ $$$${solve}\:{II}\Rightarrow\:{ma}^{\mathrm{2}} +{na}+{p} \\ $$$${solve}\:{ma}^{\mathrm{2}} +{na}+{p}=\mathrm{0} \\ $$$${a}_{\mathrm{1}} \\ $$$${a}_{\mathrm{2}} \\ $$$${DEVELOPING} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{{u}} \\ $$$$\left(\sqrt{{x}}−\sqrt{{y}}\right)\left(\sqrt{{x}}+\sqrt{{y}}\right)=\sqrt{{u}}\left(\sqrt{{x}}−\sqrt{{y}}\right) \\ $$$${x}−{y}=\sqrt{{u}}\:\left(\sqrt{{x}}−\sqrt{{y}}\right) \\ $$$$……………… \\ $$$$\sqrt{{x}}−\sqrt{{y}}=\frac{\left({x}−{y}\right)}{\:\sqrt{{u}}} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{{u}} \\ $$$$……………… \\ $$$${add} \\ $$$$\mathrm{2}\sqrt{{x}}=\frac{\left({u}+\left({x}−{y}\right)\right)}{\:\sqrt{{u}}} \\ $$$$\mathrm{4}{xu}=\left({u}+\left({x}−{y}\right)^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{yu}=\left({u}−\left({x}−{y}\right)^{\mathrm{2}} \right) \\ $$$${CONCLUSION} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{{u}} \\ $$$${is}\:{equivalent}\:{a}\:{solve} \\ $$$$\left\{\mathrm{4}{xu}=\left({u}+\left({x}−{y}\right)\right)^{\mathrm{2}} \:\:\right\}\:\cup \\ $$$$\left\{\mathrm{4}{yu}=\left({u}−\left({x}−{y}\right)\right)^{\mathrm{2}\:\:} \right\} \\ $$$$ \\ $$
Commented by manxsol last updated on 14/Dec/22
aplication (√(39−10a−a^2 ))+(√(9−a^2 ))=2(√(14)) x=39−10a−a^2 y=9−a^2 u=56 the magic : x−y=30−10a solve with 4yu=(u−(x−y))^2 (it easy) 4(56)(9−a^2 )=[56−(30−10a)]^2 4(56)(9−a^2 )=[26+10a]^2 504−56a^2 =(13+5a)^2 504−56a^2 =169+25a^2 +130a 81a^2 +130a−335=0 a_1 = 1.3837 a_2 =−2.9887 root strange
$${aplication} \\ $$$$\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }+\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{14}} \\ $$$${x}=\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} \\ $$$${y}=\mathrm{9}−{a}^{\mathrm{2}} \\ $$$${u}=\mathrm{56} \\ $$$${the}\:{magic}\:\::\:\:{x}−{y}=\mathrm{30}−\mathrm{10}{a} \\ $$$${solve}\:{with}\:\mathrm{4}{yu}=\left({u}−\left({x}−{y}\right)\right)^{\mathrm{2}} \\ $$$$\left({it}\:{easy}\right) \\ $$$$\mathrm{4}\left(\mathrm{56}\right)\left(\mathrm{9}−{a}^{\mathrm{2}} \right)=\left[\mathrm{56}−\left(\mathrm{30}−\mathrm{10}{a}\right)\right]^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{56}\right)\left(\mathrm{9}−{a}^{\mathrm{2}} \right)=\left[\mathrm{26}+\mathrm{10}{a}\right]^{\mathrm{2}} \\ $$$$\mathrm{504}−\mathrm{56}{a}^{\mathrm{2}} =\left(\mathrm{13}+\mathrm{5}{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{504}−\mathrm{56}{a}^{\mathrm{2}} =\mathrm{169}+\mathrm{25}{a}^{\mathrm{2}} +\mathrm{130}{a} \\ $$$$\mathrm{81}{a}^{\mathrm{2}} +\mathrm{130}{a}−\mathrm{335}=\mathrm{0} \\ $$$${a}_{\mathrm{1}} =\:\mathrm{1}.\mathrm{3837} \\ $$$${a}_{\mathrm{2}} =−\mathrm{2}.\mathrm{9887}\:{root}\:{strange} \\ $$$$ \\ $$$$ \\ $$
Answered by Frix last updated on 12/Dec/22
Generally: (√u)+(√v)=w Squaring and transforming ⇒ 2(√u)(√v)+v=w^2 −u−v Squaring and transforming ⇒ −4uv+(w^2 −u−v)^2 =0 Inserting u=−a^2 −10a+39∧v=−a^2 +9∧w=2(√(14)) 324a^2 +520a−1340=0 a^2 +((130a)/(81))−((335)/(81))=0 a>0 ⇒ a=((−65+56(√(10)))/(81))≈1.38379690 No “magic” possible
$$\mathrm{Generally}:\:\sqrt{{u}}+\sqrt{{v}}={w} \\ $$$$\mathrm{Squaring}\:\mathrm{and}\:\mathrm{transforming}\:\Rightarrow \\ $$$$\mathrm{2}\sqrt{{u}}\sqrt{{v}}+{v}={w}^{\mathrm{2}} −{u}−{v} \\ $$$$\mathrm{Squaring}\:\mathrm{and}\:\mathrm{transforming}\:\Rightarrow \\ $$$$−\mathrm{4}{uv}+\left({w}^{\mathrm{2}} −{u}−{v}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Inserting}\:{u}=−{a}^{\mathrm{2}} −\mathrm{10}{a}+\mathrm{39}\wedge{v}=−{a}^{\mathrm{2}} +\mathrm{9}\wedge{w}=\mathrm{2}\sqrt{\mathrm{14}} \\ $$$$\mathrm{324}{a}^{\mathrm{2}} +\mathrm{520}{a}−\mathrm{1340}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} +\frac{\mathrm{130}{a}}{\mathrm{81}}−\frac{\mathrm{335}}{\mathrm{81}}=\mathrm{0} \\ $$$${a}>\mathrm{0}\:\Rightarrow\:{a}=\frac{−\mathrm{65}+\mathrm{56}\sqrt{\mathrm{10}}}{\mathrm{81}}\approx\mathrm{1}.\mathrm{38379690} \\ $$$$\mathrm{No}\:“\mathrm{magic}''\:\mathrm{possible} \\ $$
Commented by Acem last updated on 12/Dec/22
I thought in substituation the variable but i figured out that there will be still problems I ask for a magical way if is there?
$$\:{I}\:{thought}\:{in}\:{substituation}\:{the}\:{variable}\:{but} \\ $$$$\:{i}\:{figured}\:{out}\:{that}\:{there}\:{will}\:{be}\:{still}\:{problems} \\ $$$$\:{I}\:{ask}\:{for}\:{a}\:{magical}\:{way}\:{if}\:{is}\:{there}? \\ $$
Commented by Acem last updated on 12/Dec/22
Can you show all steps?
$${Can}\:{you}\:{show}\:{all}\:{steps}? \\ $$
Commented by Frix last updated on 12/Dec/22
I inserted a few lines more
$$\mathrm{I}\:\mathrm{inserted}\:\mathrm{a}\:\mathrm{few}\:\mathrm{lines}\:\mathrm{more} \\ $$
Commented by Acem last updated on 13/Dec/22
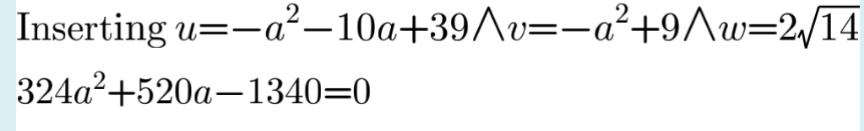
Commented by Acem last updated on 13/Dec/22
How did you make the formula?
$$\:{How}\:{did}\:{you}\:{make}\:{the}\:{formula}? \\ $$
Answered by Acem last updated on 12/Dec/22
(√(39− 10 a −a^2 )) + (√(9−a^2 )) = 2 (√(14)) (√(10(3 −a) +(9−a^2 ))) + (√(9−a^2 )) = 2(√(14)) (√(9−a^2 )) ((√((10(3−a))/(9−a^2 ))) +1)= 2(√(14)) ((10(3−a))/(9−a^2 )) +1 + 2 (√((10(3−a))/(9−a^2 ))) = ((56)/(9−a^2 )) (√((10(3−a))/(9−a^2 ))) = (1/2)[ ((56)/(9−a^2 )) − ((10(3−a))/(9−a^2 )) −1]_(making it as one term) ^(No usefull with (3−a)(3+a)) 10 = (3+a)^ × S_2 ^( 2) ^↗ etc... etc until we get rid of the root To face another complicated problems 40= (((a^2 + 10a +17)^2 )/((3−a)^2 (3+a))) ∼ Boriiiing 40= (([(a+5)^2 −8]^2 )/((3−a)^2 (3+a))) Hfff
$$\sqrt{\mathrm{39}−\:\mathrm{10}\:{a}\:−{a}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\:\mathrm{2}\:\sqrt{\mathrm{14}} \\ $$$$\:\sqrt{\mathrm{10}\left(\mathrm{3}\:−{a}\right)\:+\left(\mathrm{9}−{a}^{\mathrm{2}} \right)}\:+\:\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\:\mathrm{2}\sqrt{\mathrm{14}} \\ $$$$\:\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\left(\sqrt{\frac{\mathrm{10}\left(\mathrm{3}−{a}\right)}{\mathrm{9}−{a}^{\mathrm{2}} }}\:+\mathrm{1}\right)=\:\mathrm{2}\sqrt{\mathrm{14}} \\ $$$$\frac{\mathrm{10}\left(\mathrm{3}−{a}\right)}{\mathrm{9}−{a}^{\mathrm{2}} }\:+\mathrm{1}\:+\:\mathrm{2}\:\sqrt{\frac{\mathrm{10}\left(\mathrm{3}−{a}\right)}{\mathrm{9}−{a}^{\mathrm{2}} }}\:=\:\frac{\mathrm{56}}{\mathrm{9}−{a}^{\mathrm{2}} } \\ $$$$\sqrt{\frac{\mathrm{10}\left(\mathrm{3}−{a}\right)}{\mathrm{9}−{a}^{\mathrm{2}} }}\:=\:\underset{{making}\:{it}\:{as}\:{one}\:{term}} {\underbrace{\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{56}}{\mathrm{9}−{a}^{\mathrm{2}} }\:−\:\frac{\mathrm{10}\left(\mathrm{3}−{a}\right)}{\mathrm{9}−{a}^{\mathrm{2}} }\:\:−\mathrm{1}\right]}}\:^{{No}\:{usefull}\:{with}\:\left(\mathrm{3}−{a}\right)\left(\mathrm{3}+{a}\right)} \\ $$$$\:\mathrm{10}\:=\:\left(\mathrm{3}+{a}\right)^{\:} ×\:{S}_{\mathrm{2}} ^{\:\mathrm{2}} \:^{\nearrow} \\ $$$$\:{etc}…\:{etc}\:{until}\:{we}\:{get}\:{rid}\:{of}\:{the}\:{root} \\ $$$$\:{To}\:{face}\:{another}\:{complicated}\:{problems} \\ $$$$\:\mathrm{40}=\:\frac{\left({a}^{\mathrm{2}} +\:\mathrm{10}{a}\:+\mathrm{17}\right)^{\mathrm{2}} }{\left(\mathrm{3}−{a}\right)^{\mathrm{2}} \:\left(\mathrm{3}+{a}\right)}\:\:\:\:\:\:\:\:\sim\:{Boriiiing} \\ $$$$\:\mathrm{40}=\:\frac{\left[\left({a}+\mathrm{5}\right)^{\mathrm{2}} \:−\mathrm{8}\right]^{\mathrm{2}} }{\left(\mathrm{3}−{a}\right)^{\mathrm{2}} \:\left(\mathrm{3}+{a}\right)}\:\:\:\:\:{Hfff} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 13/Dec/22
(√(39−10a−a^2 )) +(√(9−a^2 )) =2(√(14)) _(−) ⇒∣a∣<3 ((√(39−10a−a^2 )) +(√(9−a^2 )) )((√(39−10a−a^2 )) −(√(9−a^2 )) ) =2(√(14)) ((√(39−10a−a^2 )) −(√(9−a^2 )) ) 39−10a−a^2 −9+a^2 =2(√(14)) ((√(39−10a−a^2 )) −(√(9−a^2 )) ) (√(39−10a−a^2 )) −(√(9−a^2 )) =((30−10a)/(2(√(14)))) (√(39−10a−a^2 )) −(√(9−a^2 )) =((15−5a)/( (√(14)))) determinant ((((√(39−10a−a^2 )) −(√(9−a^2 )) =((15−5a)/( (√(14))))_((√(39−10a−a^2 )) +(√(9−a^2 )) = ^( ) 2(√(14 )) ...(ii) ) ...(i)))) (ii)−(i) : 2(√(9−a^2 )) =2(√(14)) −((15−5a)/( (√(14)))) =((28−15+5a)/( (√(14))))=((13+5a)/( (√(14)))) {2((√(9−a^2 )))}^2 =(((13+5a)/( (√(14)))))^2 4(9−a^2 )=((169+130a+25a^2 )/(14)) 504−56a^2 =169+130a+25a^2 81a^2 +130a−335=0 a=((−130±(√(130^2 −4(81)(−335))))/(162)) a=((−65±56(√(10)))/(81)) a=1.3838^✓ ,−2.9888(Extraneous)
$$\underset{−} {\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:+\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\:=\mathrm{2}\sqrt{\mathrm{14}}\:\:}\: \\ $$$$\Rightarrow\mid{a}\mid<\mathrm{3}\: \\ $$$$\left(\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:+\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\right)\left(\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\right)\:=\mathrm{2}\sqrt{\mathrm{14}}\:\left(\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\right) \\ $$$$\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} −\mathrm{9}+{a}^{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{14}}\:\left(\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:\right) \\ $$$$\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\frac{\mathrm{30}−\mathrm{10}{a}}{\mathrm{2}\sqrt{\mathrm{14}}} \\ $$$$\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\frac{\mathrm{15}−\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}} \\ $$$$\begin{array}{|c|}{\underset{\overset{\:} {\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:+\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\:}\mathrm{2}\sqrt{\mathrm{14}\:}\:…\left({ii}\right)\:\:\:\:\:\:\:\:\:\:\:} {\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\frac{\mathrm{15}−\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}}}…\left({i}\right)}\\\hline\end{array} \\ $$$$\left({ii}\right)−\left({i}\right)\::\:\mathrm{2}\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\mathrm{2}\sqrt{\mathrm{14}}\:−\frac{\mathrm{15}−\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{28}−\mathrm{15}+\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}}=\frac{\mathrm{13}+\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}} \\ $$$$\left\{\mathrm{2}\left(\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\right)\right\}^{\mathrm{2}} =\left(\frac{\mathrm{13}+\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{9}−{a}^{\mathrm{2}} \right)=\frac{\mathrm{169}+\mathrm{130}{a}+\mathrm{25}{a}^{\mathrm{2}} }{\mathrm{14}} \\ $$$$\mathrm{504}−\mathrm{56}{a}^{\mathrm{2}} =\mathrm{169}+\mathrm{130}{a}+\mathrm{25}{a}^{\mathrm{2}} \\ $$$$\mathrm{81}{a}^{\mathrm{2}} +\mathrm{130}{a}−\mathrm{335}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{130}\pm\sqrt{\mathrm{130}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{81}\right)\left(−\mathrm{335}\right)}}{\mathrm{162}} \\ $$$${a}=\frac{−\mathrm{65}\pm\mathrm{56}\sqrt{\mathrm{10}}}{\mathrm{81}} \\ $$$${a}=\mathrm{1}.\mathrm{3838}^{\checkmark} ,−\mathrm{2}.\mathrm{9888}\left({Extraneous}\right) \\ $$
Commented by Acem last updated on 13/Dec/22
Weeeeee! Shokrannnn I will see the 2 your methods when finish work Thank you with all my heart!
$${Weeeeee}!\:{Shokrannnn} \\ $$$${I}\:{will}\:{see}\:{the}\:\mathrm{2}\:{your}\:{methods}\:{when}\:{finish}\:{work} \\ $$$${Thank}\:{you}\:{with}\:{all}\:{my}\:{heart}! \\ $$
Commented by Rasheed.Sindhi last updated on 13/Dec/22
You′re welcome sir!
$$\boldsymbol{\mathrm{Y}}\mathrm{ou}'\mathrm{re}\:\boldsymbol{\mathrm{w}}\mathrm{elcome}\:\boldsymbol{\mathrm{s}}\mathrm{ir}!\: \\ $$
Answered by Rasheed.Sindhi last updated on 13/Dec/22
(√(39−10a−a^2 )) _(x) +(√(9−a^2 )) _(y) =2(√(14)) x+y=2(√(14)) ......(i) x^2 −y^2 =(39−10a−a^2 )−(9−a^2 )=30−10a x−y=((x^2 −y^2 )/(x+y))=((30−10a)/(2(√(14))))=((15−5a)/( (√(14))))...(ii) (i)−(ii): 2y=2(√(14)) −((15−5a)/( (√(14))))=((28−15+5a)/( (√(14)))) y=((13+5a)/(2(√(14)))) (√(9−a^2 )) =((13+5a)/(2(√(14)))) 9−a^2 =(((13+5a)/(2(√(14)))))^2 =((169+130a+25a^2 )/(56)) 504−56a^2 =169+130a+25a^2 81a^2 +130a−335=0 a=((−130±(√(130^2 −4(81)(−335))))/(162)) =((−130±112(√(10)) )/(162)) =((−65±56(√(10)) )/(81)) =1.3838^✓ , −2.9888(Not required)
$$\underset{{x}} {\underbrace{\sqrt{\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} }\:}}+\underset{{y}} {\underbrace{\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:}}=\mathrm{2}\sqrt{\mathrm{14}} \\ $$$${x}+{y}=\mathrm{2}\sqrt{\mathrm{14}}\:……\left({i}\right) \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\left(\mathrm{39}−\mathrm{10}{a}−{a}^{\mathrm{2}} \right)−\left(\mathrm{9}−{a}^{\mathrm{2}} \right)=\mathrm{30}−\mathrm{10}{a} \\ $$$${x}−{y}=\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}+{y}}=\frac{\mathrm{30}−\mathrm{10}{a}}{\mathrm{2}\sqrt{\mathrm{14}}}=\frac{\mathrm{15}−\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}}…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right):\: \\ $$$$\mathrm{2}{y}=\mathrm{2}\sqrt{\mathrm{14}}\:−\frac{\mathrm{15}−\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}}=\frac{\mathrm{28}−\mathrm{15}+\mathrm{5}{a}}{\:\sqrt{\mathrm{14}}} \\ $$$${y}=\frac{\mathrm{13}+\mathrm{5}{a}}{\mathrm{2}\sqrt{\mathrm{14}}} \\ $$$$\sqrt{\mathrm{9}−{a}^{\mathrm{2}} }\:=\frac{\mathrm{13}+\mathrm{5}{a}}{\mathrm{2}\sqrt{\mathrm{14}}} \\ $$$$\mathrm{9}−{a}^{\mathrm{2}} =\left(\frac{\mathrm{13}+\mathrm{5}{a}}{\mathrm{2}\sqrt{\mathrm{14}}}\right)^{\mathrm{2}} =\frac{\mathrm{169}+\mathrm{130}{a}+\mathrm{25}{a}^{\mathrm{2}} }{\mathrm{56}} \\ $$$$\mathrm{504}−\mathrm{56}{a}^{\mathrm{2}} =\mathrm{169}+\mathrm{130}{a}+\mathrm{25}{a}^{\mathrm{2}} \\ $$$$\mathrm{81}{a}^{\mathrm{2}} +\mathrm{130}{a}−\mathrm{335}=\mathrm{0} \\ $$$$\:\:\:\:\:{a}=\frac{−\mathrm{130}\pm\sqrt{\mathrm{130}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{81}\right)\left(−\mathrm{335}\right)}}{\mathrm{162}} \\ $$$$\:\:\:\:\:\:\:=\frac{−\mathrm{130}\pm\mathrm{112}\sqrt{\mathrm{10}}\:}{\mathrm{162}} \\ $$$$\:\:\:\:\:\:\:=\frac{−\mathrm{65}\pm\mathrm{56}\sqrt{\mathrm{10}}\:}{\mathrm{81}} \\ $$$$\:\:\:\:\:\:=\mathrm{1}.\mathrm{3838}^{\checkmark} \:,\:−\mathrm{2}.\mathrm{9888}\left({Not}\:{required}\right) \\ $$$$ \\ $$
Commented by Acem last updated on 13/Dec/22
Thank you! dear friend
$${Thank}\:{you}!\:{dear}\:{friend} \\ $$
Commented by manxsol last updated on 13/Dec/22
wait,Sir Acem other method
$${wait},{Sir}\:{Acem}\:{other}\:{method} \\ $$
Commented by manxsol last updated on 13/Dec/22
solution not is completed
$${solution}\:{not}\:{is}\:{completed} \\ $$
Commented by manxsol last updated on 13/Dec/22
I found the magic against boredom
$${I}\:{found}\:{the}\:{magic}\:{against}\:{boredom} \\ $$
Answered by mr W last updated on 14/Dec/22
Commented by mr W last updated on 13/Dec/22
geometric method (√(39−10x−x^2 ))+(√(9−x^2 ))=2(√(14)) ⇒(√(8^2 −(5+x)^2 ))+(√(3^2 −x^2 ))=2(√(14)) the geometric meaning of this equation see diagram above. (√(5^2 +(2(√(14)))^2 ))=9 sin α=(5/9) ⇒cos α=((2(√(14)))/9) cos β=((8^2 +9^2 −3^2 )/(2×8×9))=((17)/(18)) ⇒sin β=((√(35))/(18)) 5+x=8 sin (α+β) =8 ((5/9)×((17)/(18))+((2(√(14)))/9)×((√(35))/(18))) =((4(85+14(√(10))))/(81)) ⇒x=((4(85+14(√(10))))/(81))−5=((56(√(10))−65)/(81)) ✓
$$\underline{\boldsymbol{{geometric}}\:\boldsymbol{{method}}} \\ $$$$ \\ $$$$\sqrt{\mathrm{39}−\mathrm{10}{x}−{x}^{\mathrm{2}} }+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{14}} \\ $$$$\Rightarrow\sqrt{\mathrm{8}^{\mathrm{2}} −\left(\mathrm{5}+{x}\right)^{\mathrm{2}} }+\sqrt{\mathrm{3}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{14}} \\ $$$${the}\:{geometric}\:{meaning}\:{of}\:{this} \\ $$$${equation}\:{see}\:{diagram}\:{above}. \\ $$$$\sqrt{\mathrm{5}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{14}}\right)^{\mathrm{2}} }=\mathrm{9} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{5}}{\mathrm{9}}\:\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{14}}}{\mathrm{9}} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{8}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×\mathrm{9}}=\frac{\mathrm{17}}{\mathrm{18}}\:\Rightarrow\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{35}}}{\mathrm{18}} \\ $$$$\mathrm{5}+{x}=\mathrm{8}\:\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{8}\:\left(\frac{\mathrm{5}}{\mathrm{9}}×\frac{\mathrm{17}}{\mathrm{18}}+\frac{\mathrm{2}\sqrt{\mathrm{14}}}{\mathrm{9}}×\frac{\sqrt{\mathrm{35}}}{\mathrm{18}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\left(\mathrm{85}+\mathrm{14}\sqrt{\mathrm{10}}\right)}{\mathrm{81}} \\ $$$$\:\Rightarrow{x}=\frac{\mathrm{4}\left(\mathrm{85}+\mathrm{14}\sqrt{\mathrm{10}}\right)}{\mathrm{81}}−\mathrm{5}=\frac{\mathrm{56}\sqrt{\mathrm{10}}−\mathrm{65}}{\mathrm{81}}\:\checkmark \\ $$
Commented by manxsol last updated on 14/Dec/22
you are great!
$${you}\:{are}\:{great}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *