Question Number 100866 by mathmax by abdo last updated on 29/Jun/20
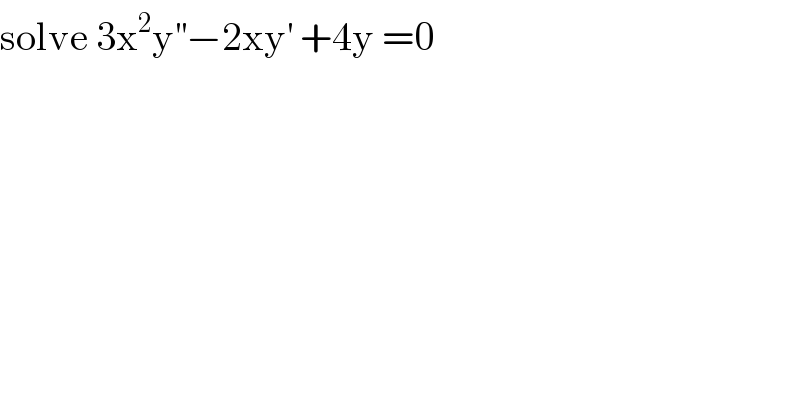
$$\mathrm{solve}\:\mathrm{3x}^{\mathrm{2}} \mathrm{y}^{''} −\mathrm{2xy}^{'} \:+\mathrm{4y}\:=\mathrm{0} \\ $$
Answered by bramlex last updated on 29/Jun/20
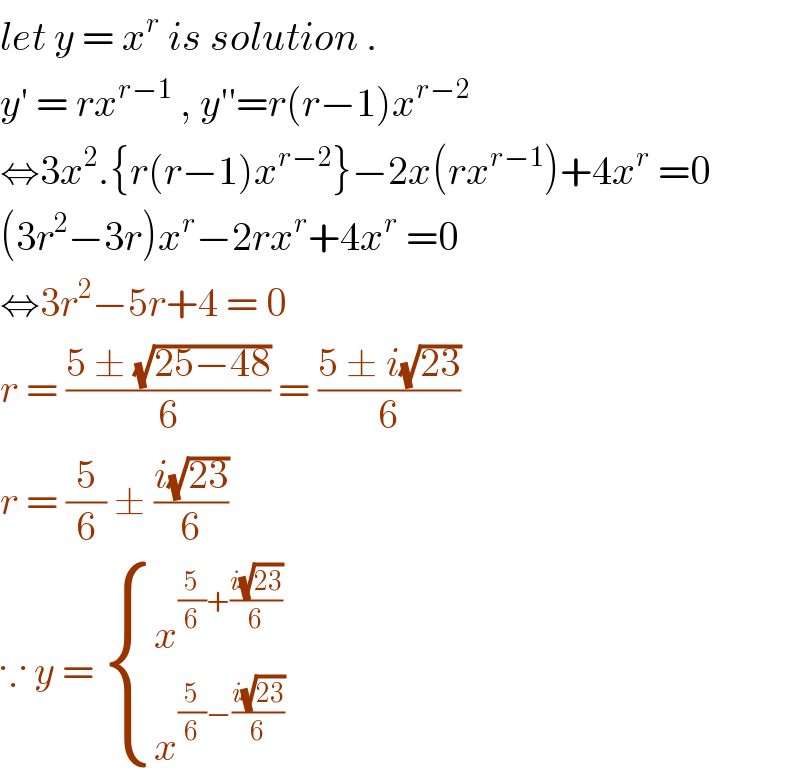
$${let}\:{y}\:=\:{x}^{{r}} \:{is}\:{solution}\:. \\ $$$${y}'\:=\:{rx}^{{r}−\mathrm{1}} \:,\:{y}''={r}\left({r}−\mathrm{1}\right){x}^{{r}−\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{3}{x}^{\mathrm{2}} .\left\{{r}\left({r}−\mathrm{1}\right){x}^{{r}−\mathrm{2}} \right\}−\mathrm{2}{x}\left({rx}^{{r}−\mathrm{1}} \right)+\mathrm{4}{x}^{{r}} \:=\mathrm{0} \\ $$$$\left(\mathrm{3}{r}^{\mathrm{2}} −\mathrm{3}{r}\right){x}^{{r}} −\mathrm{2}{rx}^{{r}} +\mathrm{4}{x}^{{r}} \:=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{3}{r}^{\mathrm{2}} −\mathrm{5}{r}+\mathrm{4}\:=\:\mathrm{0} \\ $$$${r}\:=\:\frac{\mathrm{5}\:\pm\:\sqrt{\mathrm{25}−\mathrm{48}}}{\mathrm{6}}\:=\:\frac{\mathrm{5}\:\pm\:{i}\sqrt{\mathrm{23}}}{\mathrm{6}} \\ $$$${r}\:=\:\frac{\mathrm{5}}{\mathrm{6}}\:\pm\:\frac{{i}\sqrt{\mathrm{23}}}{\mathrm{6}} \\ $$$$\because\:{y}\:=\:\begin{cases}{{x}^{\frac{\mathrm{5}}{\mathrm{6}}+\frac{{i}\sqrt{\mathrm{23}}}{\mathrm{6}}} }\\{{x}^{\frac{\mathrm{5}}{\mathrm{6}}−\frac{{i}\sqrt{\mathrm{23}}}{\mathrm{6}}} }\end{cases} \\ $$
