Question Number 93470 by I want to learn more last updated on 13/May/20
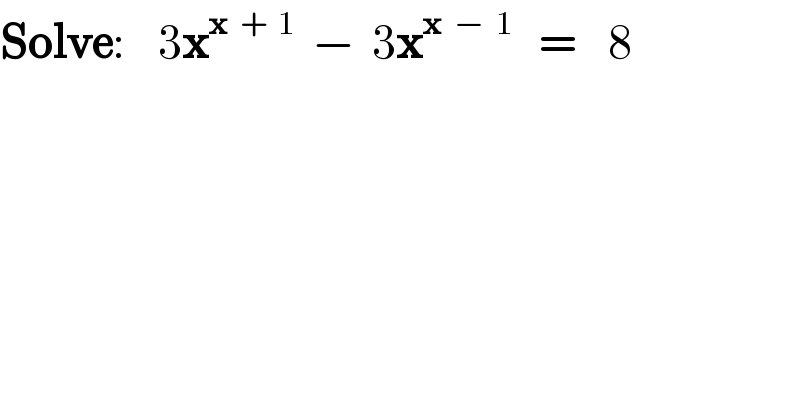
$$\boldsymbol{\mathrm{Solve}}:\:\:\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:+\:\:\mathrm{1}} \:\:−\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:−\:\:\mathrm{1}} \:\:\:=\:\:\:\:\mathrm{8} \\ $$
Commented by i jagooll last updated on 13/May/20

$$\mathrm{aproximate} \\ $$$$\mathrm{x}\approx\:\mathrm{1}.\mathrm{6901049597962} \\ $$
Commented by I want to learn more last updated on 13/May/20
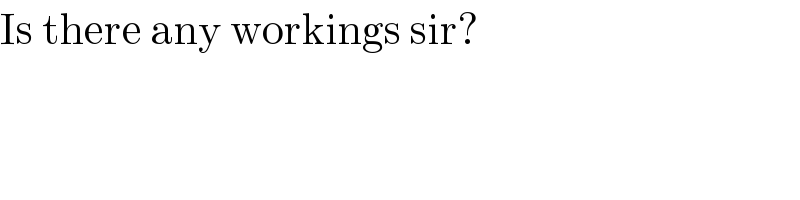
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{workings}\:\mathrm{sir}? \\ $$
Commented by john santu last updated on 13/May/20

Commented by john santu last updated on 13/May/20

$$\mathrm{sir}\:\mathrm{jagool}\:\mathrm{is}\:\mathrm{correct}\: \\ $$
Answered by Rasheed.Sindhi last updated on 13/May/20
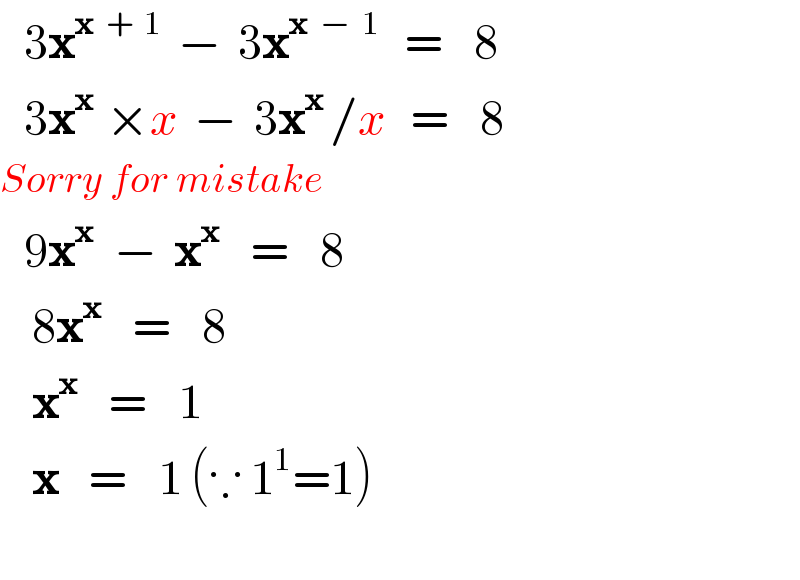
$$\:\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:+\:\:\mathrm{1}} \:\:−\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:−\:\:\mathrm{1}} \:\:\:=\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:} ×{x}\:\:−\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:} /{x}\:\:\:=\:\:\:\:\mathrm{8} \\ $$$${Sorry}\:{for}\:{mistake} \\ $$$$\:\:\:\mathrm{9}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:\:} \:−\:\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:} \:\:\:=\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\:\mathrm{8}\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:} \:\:\:=\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}\:} \:\:\:=\:\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}^{\:} \:\:\:=\:\:\:\:\mathrm{1}\:\left(\because\:\mathrm{1}^{\mathrm{1}} =\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Commented by i jagooll last updated on 13/May/20
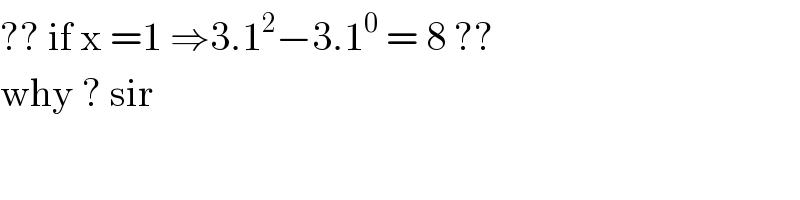
$$??\:\mathrm{if}\:\mathrm{x}\:=\mathrm{1}\:\Rightarrow\mathrm{3}.\mathrm{1}^{\mathrm{2}} −\mathrm{3}.\mathrm{1}^{\mathrm{0}} \:=\:\mathrm{8}\:?? \\ $$$$\mathrm{why}\:?\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 13/May/20
$${Sorry}\:{for}\:{mistake}. \\ $$
