Question Number 18036 by tawa tawa last updated on 14/Jul/17
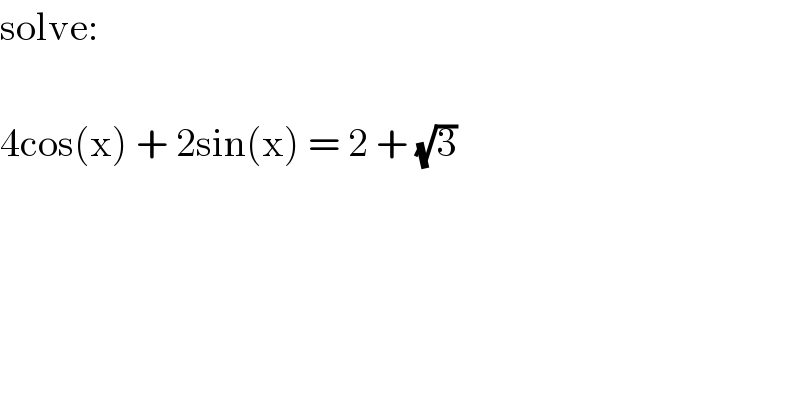
$$\mathrm{solve}: \\ $$$$ \\ $$$$\mathrm{4cos}\left(\mathrm{x}\right)\:+\:\mathrm{2sin}\left(\mathrm{x}\right)\:=\:\mathrm{2}\:+\:\sqrt{\mathrm{3}} \\ $$
Commented by ajfour last updated on 14/Jul/17
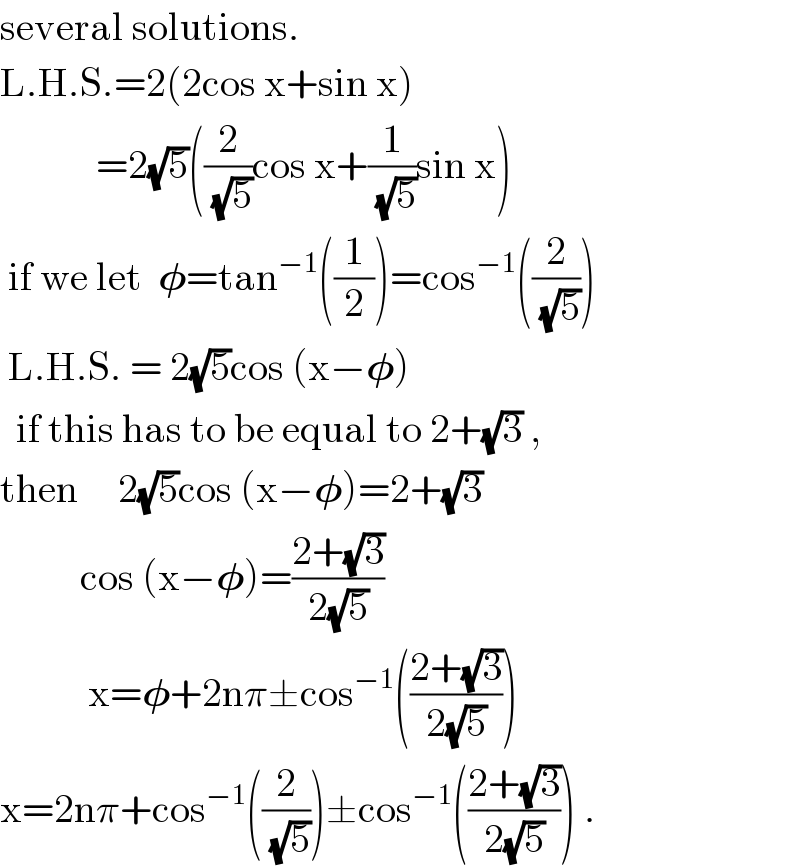
$$\mathrm{several}\:\mathrm{solutions}. \\ $$$$\mathrm{L}.\mathrm{H}.\mathrm{S}.=\mathrm{2}\left(\mathrm{2cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{5}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:\:\boldsymbol{\phi}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\:\mathrm{L}.\mathrm{H}.\mathrm{S}.\:=\:\mathrm{2}\sqrt{\mathrm{5}}\mathrm{cos}\:\left(\mathrm{x}−\boldsymbol{\phi}\right) \\ $$$$\:\:\mathrm{if}\:\mathrm{this}\:\mathrm{has}\:\mathrm{to}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2}+\sqrt{\mathrm{3}}\:, \\ $$$$\mathrm{then}\:\:\:\:\:\mathrm{2}\sqrt{\mathrm{5}}\mathrm{cos}\:\left(\mathrm{x}−\boldsymbol{\phi}\right)=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\left(\mathrm{x}−\boldsymbol{\phi}\right)=\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\boldsymbol{\phi}+\mathrm{2n}\pi\pm\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{5}}}\right) \\ $$$$\mathrm{x}=\mathrm{2n}\pi+\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\pm\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{5}}}\right)\:. \\ $$
Commented by tawa tawa last updated on 14/Jul/17

$$\mathrm{please}\:\mathrm{workings} \\ $$
Commented by ajfour last updated on 14/Jul/17
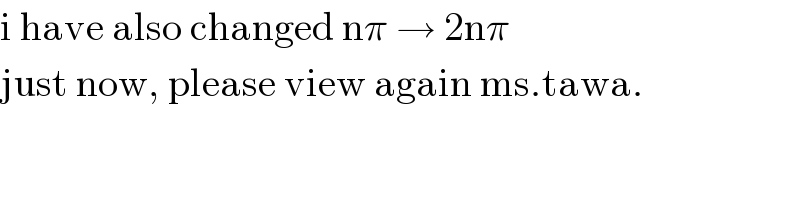
$$\mathrm{i}\:\mathrm{have}\:\mathrm{also}\:\mathrm{changed}\:\mathrm{n}\pi\:\rightarrow\:\mathrm{2n}\pi \\ $$$$\mathrm{just}\:\mathrm{now},\:\mathrm{please}\:\mathrm{view}\:\mathrm{again}\:\mathrm{ms}.\mathrm{tawa}. \\ $$
Commented by tawa tawa last updated on 14/Jul/17
$$\mathrm{Seen}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
