Question Number 170203 by bounhome last updated on 18/May/22
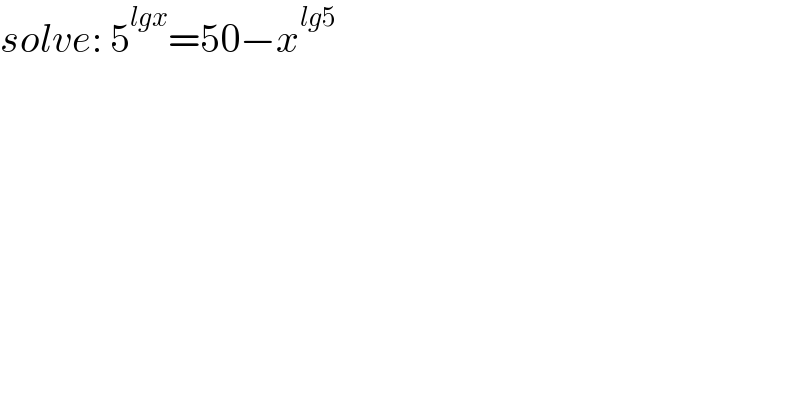
$${solve}:\:\mathrm{5}^{{lgx}} =\mathrm{50}−{x}^{{lg}\mathrm{5}} \\ $$
Answered by aleks041103 last updated on 18/May/22
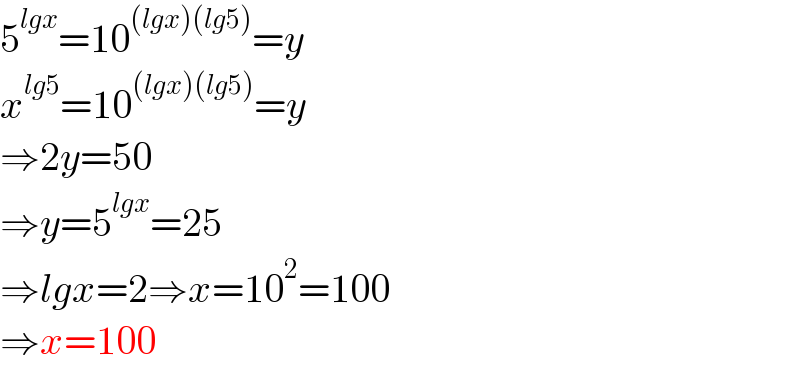
$$\mathrm{5}^{{lgx}} =\mathrm{10}^{\left({lgx}\right)\left({lg}\mathrm{5}\right)} ={y} \\ $$$${x}^{{lg}\mathrm{5}} =\mathrm{10}^{\left({lgx}\right)\left({lg}\mathrm{5}\right)} ={y} \\ $$$$\Rightarrow\mathrm{2}{y}=\mathrm{50} \\ $$$$\Rightarrow{y}=\mathrm{5}^{{lgx}} =\mathrm{25} \\ $$$$\Rightarrow{lgx}=\mathrm{2}\Rightarrow{x}=\mathrm{10}^{\mathrm{2}} =\mathrm{100} \\ $$$$\Rightarrow{x}=\mathrm{100} \\ $$
