Question Number 172182 by Mikenice last updated on 23/Jun/22

$${solve} \\ $$$$\mathrm{6}^{{x}} +\mathrm{6}^{{y}} =\mathrm{42} \\ $$$${x}+{y}=\mathrm{3} \\ $$
Answered by mr W last updated on 24/Jun/22
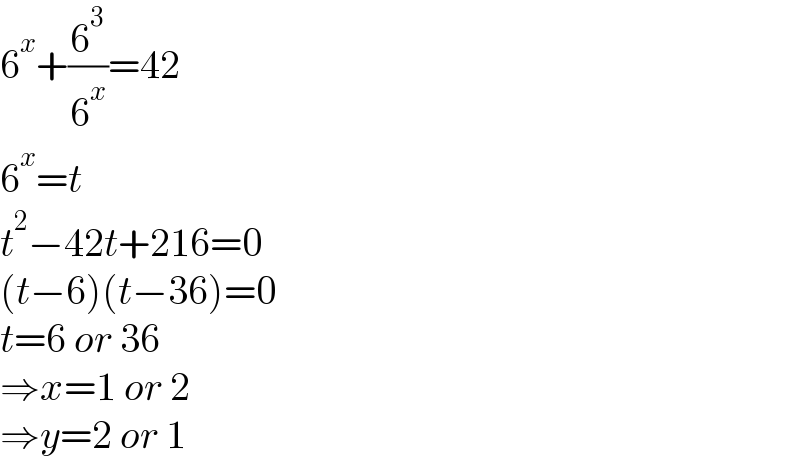
$$\mathrm{6}^{{x}} +\frac{\mathrm{6}^{\mathrm{3}} }{\mathrm{6}^{{x}} }=\mathrm{42} \\ $$$$\mathrm{6}^{{x}} ={t} \\ $$$${t}^{\mathrm{2}} −\mathrm{42}{t}+\mathrm{216}=\mathrm{0} \\ $$$$\left({t}−\mathrm{6}\right)\left({t}−\mathrm{36}\right)=\mathrm{0} \\ $$$${t}=\mathrm{6}\:{or}\:\mathrm{36} \\ $$$$\Rightarrow{x}=\mathrm{1}\:{or}\:\mathrm{2} \\ $$$$\Rightarrow{y}=\mathrm{2}\:{or}\:\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jun/22
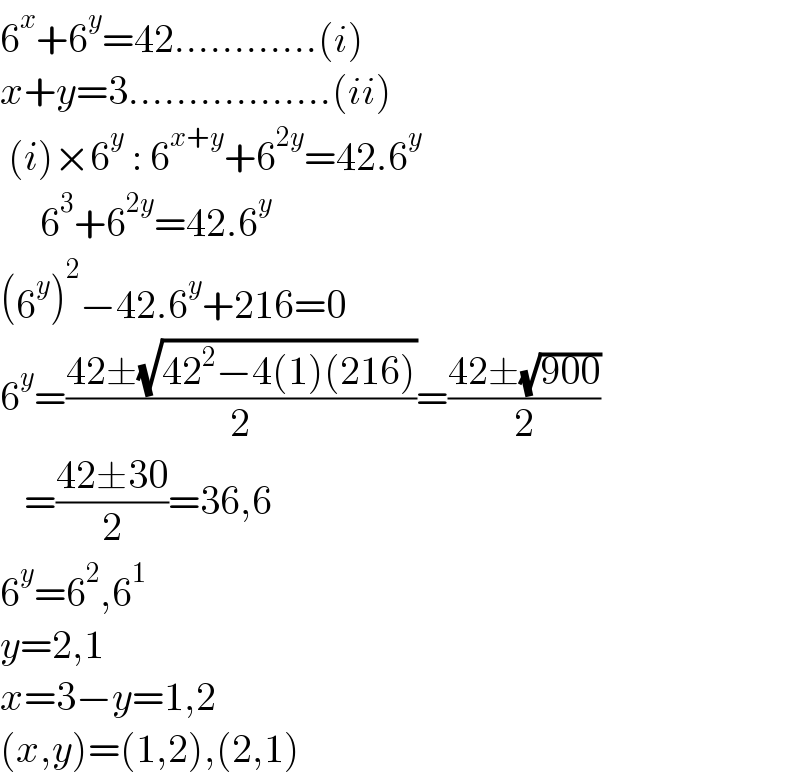
$$\mathrm{6}^{{x}} +\mathrm{6}^{{y}} =\mathrm{42}…………\left({i}\right) \\ $$$${x}+{y}=\mathrm{3}……………..\left({ii}\right) \\ $$$$\:\left({i}\right)×\mathrm{6}^{{y}} \::\:\mathrm{6}^{{x}+{y}} +\mathrm{6}^{\mathrm{2}{y}} =\mathrm{42}.\mathrm{6}^{{y}} \\ $$$$\:\:\:\:\:\mathrm{6}^{\mathrm{3}} +\mathrm{6}^{\mathrm{2}{y}} =\mathrm{42}.\mathrm{6}^{{y}} \\ $$$$\left(\mathrm{6}^{{y}} \right)^{\mathrm{2}} −\mathrm{42}.\mathrm{6}^{{y}} +\mathrm{216}=\mathrm{0} \\ $$$$\mathrm{6}^{{y}} =\frac{\mathrm{42}\pm\sqrt{\mathrm{42}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{216}\right)}}{\mathrm{2}}=\frac{\mathrm{42}\pm\sqrt{\mathrm{900}}}{\mathrm{2}} \\ $$$$\:\:\:=\frac{\mathrm{42}\pm\mathrm{30}}{\mathrm{2}}=\mathrm{36},\mathrm{6} \\ $$$$\mathrm{6}^{{y}} =\mathrm{6}^{\mathrm{2}} ,\mathrm{6}^{\mathrm{1}} \\ $$$${y}=\mathrm{2},\mathrm{1} \\ $$$${x}=\mathrm{3}−{y}=\mathrm{1},\mathrm{2} \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right) \\ $$
