Question Number 118954 by bramlexs22 last updated on 21/Oct/20
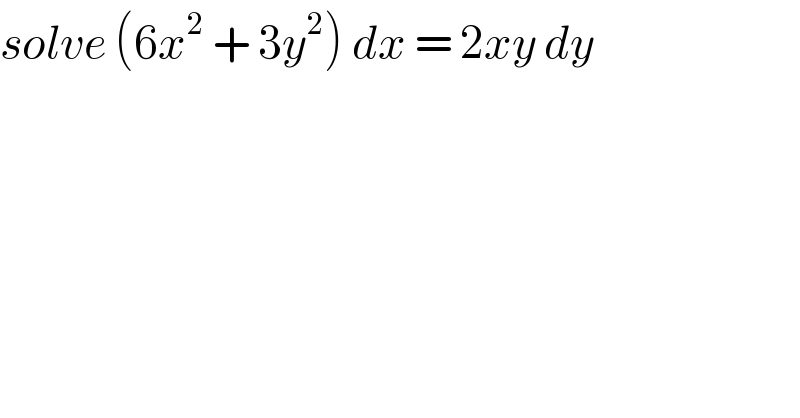
$${solve}\:\left(\mathrm{6}{x}^{\mathrm{2}} \:+\:\mathrm{3}{y}^{\mathrm{2}} \right)\:{dx}\:=\:\mathrm{2}{xy}\:{dy} \\ $$
Answered by john santu last updated on 21/Oct/20
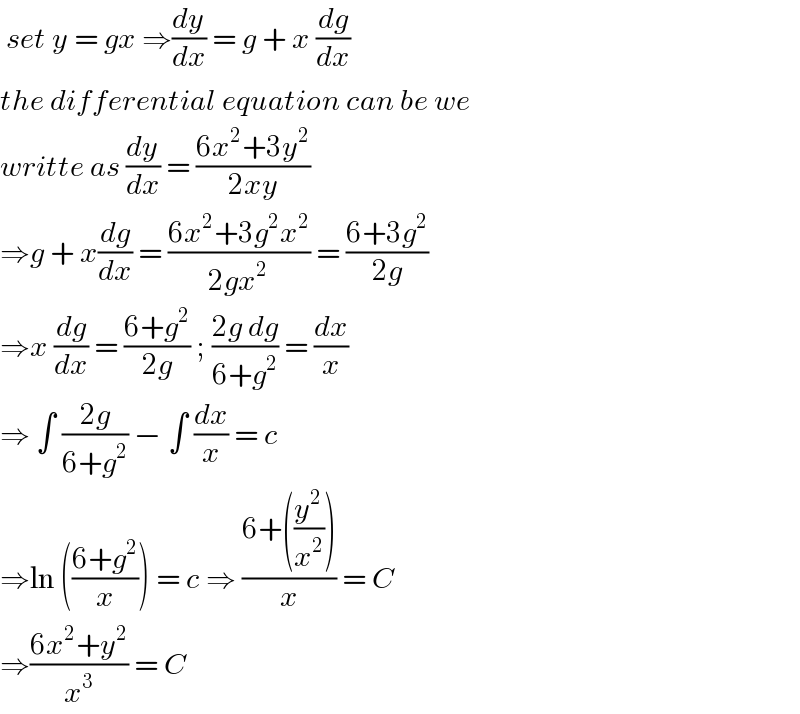
$$\:{set}\:{y}\:=\:{gx}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:{g}\:+\:{x}\:\frac{{dg}}{{dx}} \\ $$$${the}\:{differential}\:{equation}\:{can}\:{be}\:{we} \\ $$$${writte}\:{as}\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{2}{xy}} \\ $$$$\Rightarrow{g}\:+\:{x}\frac{{dg}}{{dx}}\:=\:\frac{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{3}{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gx}^{\mathrm{2}} }\:=\:\frac{\mathrm{6}+\mathrm{3}{g}^{\mathrm{2}} }{\mathrm{2}{g}} \\ $$$$\Rightarrow{x}\:\frac{{dg}}{{dx}}\:=\:\frac{\mathrm{6}+{g}^{\mathrm{2}} }{\mathrm{2}{g}}\:;\:\frac{\mathrm{2}{g}\:{dg}}{\mathrm{6}+{g}^{\mathrm{2}} }\:=\:\frac{{dx}}{{x}} \\ $$$$\Rightarrow\:\int\:\frac{\mathrm{2}{g}}{\mathrm{6}+{g}^{\mathrm{2}} }\:−\:\int\:\frac{{dx}}{{x}}\:=\:{c}\: \\ $$$$\Rightarrow\mathrm{ln}\:\left(\frac{\mathrm{6}+{g}^{\mathrm{2}} }{{x}}\right)\:=\:{c}\:\Rightarrow\:\frac{\mathrm{6}+\left(\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}{{x}}\:=\:{C} \\ $$$$\Rightarrow\frac{\mathrm{6}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{x}^{\mathrm{3}} }\:=\:{C}\: \\ $$
Answered by 1549442205PVT last updated on 21/Oct/20
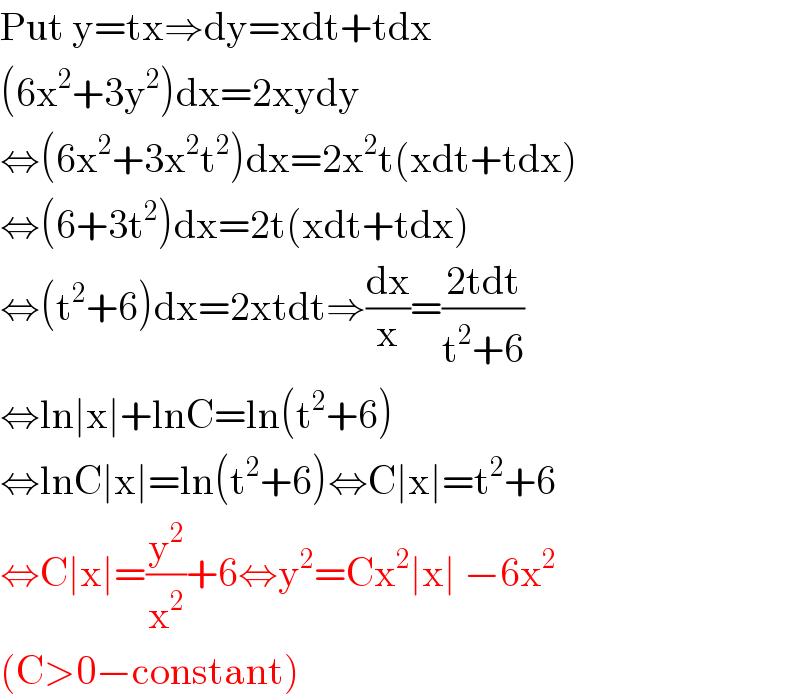
$$\mathrm{Put}\:\mathrm{y}=\mathrm{tx}\Rightarrow\mathrm{dy}=\mathrm{xdt}+\mathrm{tdx} \\ $$$$\left(\mathrm{6x}^{\mathrm{2}} +\mathrm{3y}^{\mathrm{2}} \right)\mathrm{dx}=\mathrm{2xydy} \\ $$$$\Leftrightarrow\left(\mathrm{6x}^{\mathrm{2}} +\mathrm{3x}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} \right)\mathrm{dx}=\mathrm{2x}^{\mathrm{2}} \mathrm{t}\left(\mathrm{xdt}+\mathrm{tdx}\right) \\ $$$$\Leftrightarrow\left(\mathrm{6}+\mathrm{3t}^{\mathrm{2}} \right)\mathrm{dx}=\mathrm{2t}\left(\mathrm{xdt}+\mathrm{tdx}\right) \\ $$$$\Leftrightarrow\left(\mathrm{t}^{\mathrm{2}} +\mathrm{6}\right)\mathrm{dx}=\mathrm{2xtdt}\Rightarrow\frac{\mathrm{dx}}{\mathrm{x}}=\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{6}} \\ $$$$\Leftrightarrow\mathrm{ln}\mid\mathrm{x}\mid+\mathrm{lnC}=\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{6}\right) \\ $$$$\Leftrightarrow\mathrm{lnC}\mid\mathrm{x}\mid=\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{6}\right)\Leftrightarrow\mathrm{C}\mid\mathrm{x}\mid=\mathrm{t}^{\mathrm{2}} +\mathrm{6} \\ $$$$\Leftrightarrow\mathrm{C}\mid\mathrm{x}\mid=\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }+\mathrm{6}\Leftrightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{Cx}^{\mathrm{2}} \mid\mathrm{x}\mid\:−\mathrm{6x}^{\mathrm{2}} \\ $$$$\left(\mathrm{C}>\mathrm{0}−\mathrm{constant}\right) \\ $$
