Question Number 114653 by bemath last updated on 20/Sep/20
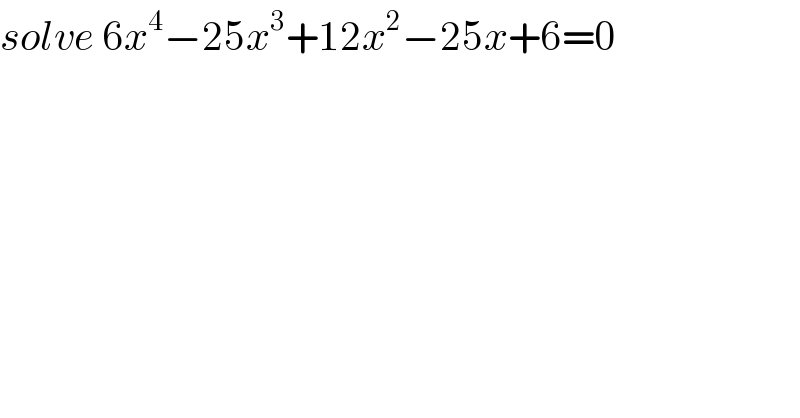
$${solve}\:\mathrm{6}{x}^{\mathrm{4}} −\mathrm{25}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} −\mathrm{25}{x}+\mathrm{6}=\mathrm{0} \\ $$
Answered by bobhans last updated on 20/Sep/20

$$\Leftrightarrow\mathrm{6}\left({x}^{\mathrm{4}} +\mathrm{1}\right)−\mathrm{25}\left({x}^{\mathrm{3}} +{x}\right)+\mathrm{12}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${assume}\:{x}\:\neq\:\mathrm{0} \\ $$$$\mathrm{6}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{25}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{12}=\mathrm{0} \\ $$$${let}\:{x}+\frac{\mathrm{1}}{{x}}\:=\:{b} \\ $$$$\Leftrightarrow\:\mathrm{6}\left({b}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{25}{b}+\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{6}{b}^{\mathrm{2}} −\mathrm{25}{b}\:=\:\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{b}=\mathrm{0}\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=\mathrm{0};\:{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0};\:{x}=\pm{i}}\\{{b}=\frac{\mathrm{25}}{\mathrm{6}}\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=\frac{\mathrm{25}}{\mathrm{6}};\mathrm{6}{x}^{\mathrm{2}} −\mathrm{25}{x}+\mathrm{6}=\mathrm{0}}\end{cases} \\ $$$$\:{x}\:=\:\frac{\mathrm{25}\:\pm\:\sqrt{\mathrm{625}−\mathrm{144}}}{\mathrm{12}}\:=\:\frac{\mathrm{25}\:\pm\:\sqrt{\mathrm{481}}}{\mathrm{12}} \\ $$
Answered by MJS_new last updated on 20/Sep/20
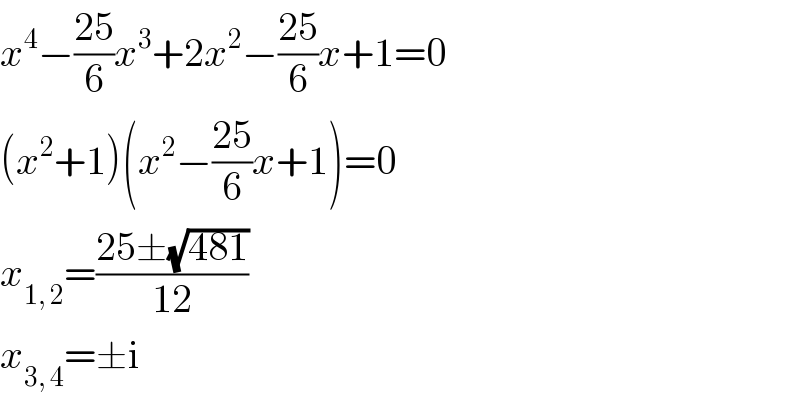
$${x}^{\mathrm{4}} −\frac{\mathrm{25}}{\mathrm{6}}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{6}}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{6}}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\frac{\mathrm{25}\pm\sqrt{\mathrm{481}}}{\mathrm{12}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\pm\mathrm{i} \\ $$
Commented by bobhans last updated on 21/Sep/20
$${gave}\:{kudos}\:{sir}\:{MJS}\:−{new} \\ $$
