Question Number 87009 by mr W last updated on 01/Apr/20
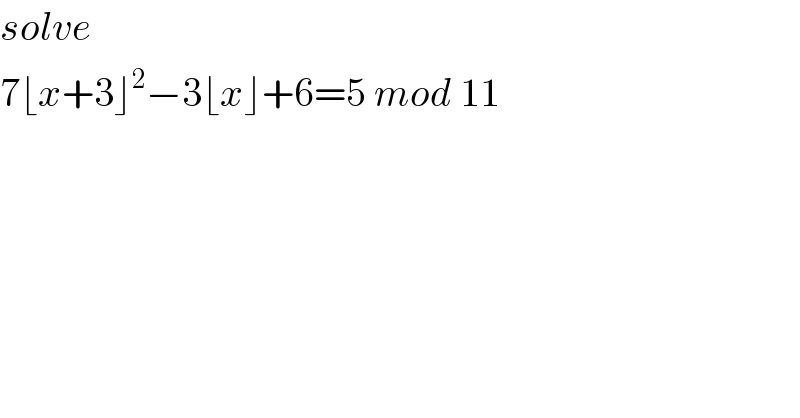
$${solve} \\ $$$$\mathrm{7}\lfloor{x}+\mathrm{3}\rfloor^{\mathrm{2}} −\mathrm{3}\lfloor{x}\rfloor+\mathrm{6}=\mathrm{5}\:{mod}\:\mathrm{11} \\ $$
Answered by MJS last updated on 01/Apr/20
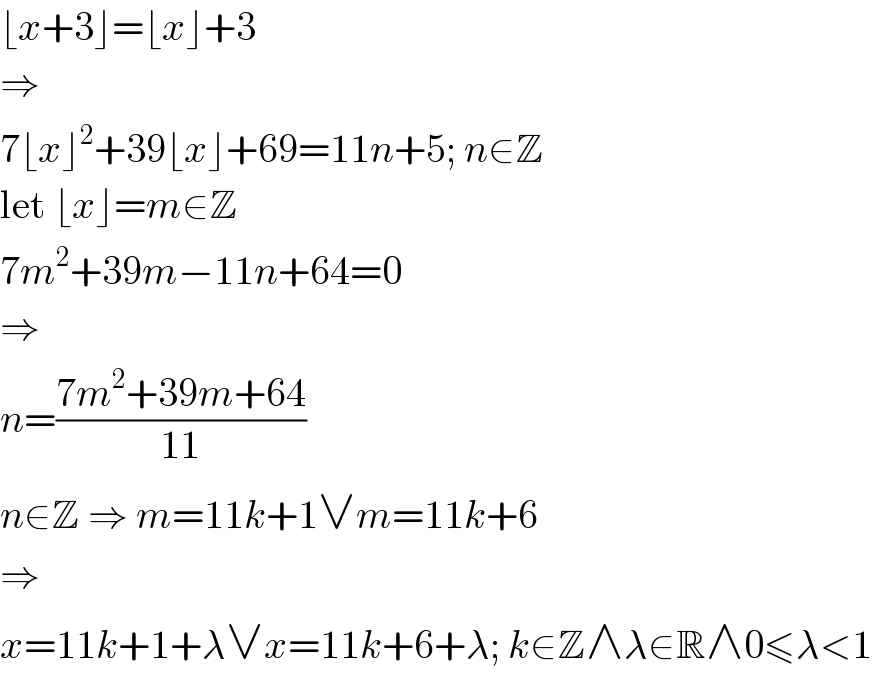
$$\lfloor{x}+\mathrm{3}\rfloor=\lfloor{x}\rfloor+\mathrm{3} \\ $$$$\Rightarrow \\ $$$$\mathrm{7}\lfloor{x}\rfloor^{\mathrm{2}} +\mathrm{39}\lfloor{x}\rfloor+\mathrm{69}=\mathrm{11}{n}+\mathrm{5};\:{n}\in\mathbb{Z} \\ $$$$\mathrm{let}\:\lfloor{x}\rfloor={m}\in\mathbb{Z} \\ $$$$\mathrm{7}{m}^{\mathrm{2}} +\mathrm{39}{m}−\mathrm{11}{n}+\mathrm{64}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${n}=\frac{\mathrm{7}{m}^{\mathrm{2}} +\mathrm{39}{m}+\mathrm{64}}{\mathrm{11}} \\ $$$${n}\in\mathbb{Z}\:\Rightarrow\:{m}=\mathrm{11}{k}+\mathrm{1}\vee{m}=\mathrm{11}{k}+\mathrm{6} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{11}{k}+\mathrm{1}+\lambda\vee{x}=\mathrm{11}{k}+\mathrm{6}+\lambda;\:{k}\in\mathbb{Z}\wedge\lambda\in\mathbb{R}\wedge\mathrm{0}\leqslant\lambda<\mathrm{1} \\ $$
Answered by M±th+et£s last updated on 02/Apr/20

