Menu Close

Solve-a-2-c-2-196-i-b-2-c-a-2-169-ii-c-2-b-c-2-225-iii-

Tinku Tara 0 Comments
Pin




Question Number 104377 by I want to learn more last updated on 21/Jul/20
Solve: a^2 + c^2 = 196 ... (i) b^2 + (c − a)^2 = 169 ... (ii) c^2 + (b − c)^2 = 225 .... (iii)
$$\mathrm{Solve}:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} \:\:+\:\mathrm{c}^{\mathrm{2}} \:\:=\:\:\mathrm{196}\:\:\:\:\:\:\:\:…\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{c}\:\:−\:\:\mathrm{a}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{169}\:\:\:…\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{b}\:\:−\:\:\mathrm{c}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{225}\:\:\:\:\:….\:\left(\mathrm{iii}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jul/20
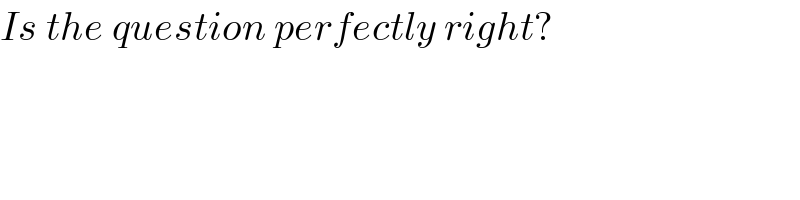
Is the question perfectly right?
$${Is}\:{the}\:{question}\:{perfectly}\:{right}? \\ $$
Commented by 1549442205PVT last updated on 21/Jul/20
Three equatios for three unknowns I think that it is perfect
$$\mathrm{Three}\:\mathrm{equatios}\:\mathrm{for}\:\mathrm{three}\:\mathrm{unknowns} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{perfect} \\ $$
Commented by I want to learn more last updated on 21/Jul/20
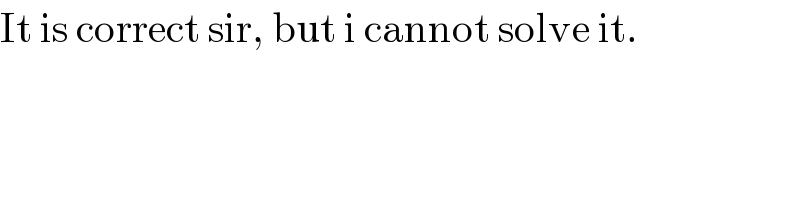
It is correct sir, but i cannot solve it.
$$\mathrm{It}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{i}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{it}. \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jul/20
The question may be as: a^2 + c^2 = 196 ... (i) b^2 +(c−a)^2 = 169 ... (ii) c^2 +(b−a)^2 = 225 .... (iii) Or as a^2 +(b−c)^2 = 196 ... (i) b^2 +(c−a)^2 = 169 ... (ii) c^2 +(b−a)^2 = 225 .... (iii) ?????
$$\mathcal{T}{he}\:{question}\:{may}\:{be}\:{as}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} +\:\mathrm{c}^{\mathrm{2}} \:\:=\:\:\mathrm{196}\:\:\:\:\:\:\:\:…\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}^{\mathrm{2}} +\left(\mathrm{c}−\mathrm{a}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{169}\:\:\:…\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}^{\mathrm{2}} +\left(\mathrm{b}−\mathrm{a}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{225}\:\:\:\:\:….\:\left(\mathrm{iii}\right) \\ $$$${Or}\:{as} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} +\left({b}−{c}\right)^{\mathrm{2}} \:=\:\:\mathrm{196}\:\:\:\:\:\:\:\:…\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}^{\mathrm{2}} +\left(\mathrm{c}−\mathrm{a}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{169}\:\:\:…\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}^{\mathrm{2}} +\left(\mathrm{b}−\mathrm{a}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{225}\:\:\:\:\:….\:\left(\mathrm{iii}\right) \\ $$$$\:\:\:\:\:????? \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jul/20
Thanks Sir!
$$\mathcal{T}{hanks}\:\mathcal{S}{ir}! \\ $$
Commented by I want to learn more last updated on 22/Jul/20
Not (b − a)^(2 ) sir. (b − c)^2 .
$$\mathrm{Not}\:\:\left(\mathrm{b}\:\:−\:\:\mathrm{a}\right)^{\mathrm{2}\:\:\:} \mathrm{sir}.\:\:\:\:\:\left(\mathrm{b}\:\:−\:\:\mathrm{c}\right)^{\mathrm{2}} . \\ $$
Answered by 1549442205PVT last updated on 23/Jul/20
From (i) and (ii)we get b^2 +c^2 +a^2 −2ac=169⇒b^2 −2ac=−27 ⇒a=((b^2 +27)/(2c))(1)⇒a^2 =((b^4 +54b^2 +729)/(4c^2 )).Replace into (i)we get b^4 +54b^2 +4c^4 −784c^2 =0(2) From(iii)we get b=c±(√(225−c^2 )) (3) ⇒b^2 =225±2c(√(225−c^2 )) (4) b^4 =50626±900c(√(225−c^2 )) +900c^2 −4c^4 (5) Replace(4)(5) into (2) we get 50625±900c(√(225−c^2 )) +900c^2 −4c^4 + 12150±108c(√(225−c^2 ))+729+4c^4 −784c^2 +900c^2 −4c^4 =0 ⇔116c^2 +63504±1008c(√(225−c^2 )) =0 ⇒116c^2 +63504=±1008c(√(225−c^2 )) . Squaring two sides of the above eqs.we get 13456c^4 +14 732 928c^2 +4 032 758 016=1 016 064c^2 (225−c^2 ) ⇔1 029 520c^4 −213 881 472c^2 +4 032 758 016=0(6) Solve (6) by caculator we get c^2 ∈{((15876)/(85));((15876)/(757))}⇒c∈{±13.66661884,±4.57954789} a)For c=13.66661884 from (3)we get b∈{19.84913689,7.484100795}.Replace into(1)we get a∈{15.4020625,3.03702641} Check directly we see only the triple (a,b,c)=(3.0370;7.484;13.6666}is accepted b)For c=4.579547894,similarly we get (a,b,c)=(13.22980;−9.7042800;4.5795) c)For c=−13.66661884 from (3)we get b∈{−7.484100795,−19.84913689} a∈{−3.03702641,−15.4020625} (a,b,c)=(−3.037,−7.4841,−13.6666) d)For c=−4.57954789 we get b∈{9.704280069,−18.86337585} a∈{−13.22980503,−41.79746098} (a,b,c)=(−13.22980,9.70428,−4.5795) Thus,we get four triples (a,b,c) satisfy the given system of the equtions
$$\mathrm{From}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{2ac}=\mathrm{169}\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{2ac}=−\mathrm{27} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{27}}{\mathrm{2c}}\left(\mathrm{1}\right)\Rightarrow\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{b}^{\mathrm{4}} +\mathrm{54b}^{\mathrm{2}} +\mathrm{729}}{\mathrm{4c}^{\mathrm{2}} }.\mathrm{Replace}\:\mathrm{into} \\ $$$$\left(\mathrm{i}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{b}^{\mathrm{4}} +\mathrm{54b}^{\mathrm{2}} +\mathrm{4c}^{\mathrm{4}} −\mathrm{784c}^{\mathrm{2}} =\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\mathrm{iii}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{b}=\mathrm{c}\pm\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} \:}\:\left(\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} =\mathrm{225}\pm\mathrm{2c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} }\:\left(\mathrm{4}\right) \\ $$$$\mathrm{b}^{\mathrm{4}} =\mathrm{50626}\pm\mathrm{900c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} }\:+\mathrm{900c}^{\mathrm{2}} −\mathrm{4c}^{\mathrm{4}} \left(\mathrm{5}\right) \\ $$$$\mathrm{Replace}\left(\mathrm{4}\right)\left(\mathrm{5}\right)\:\mathrm{into}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{50625}\pm\mathrm{900c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} }\:+\mathrm{900c}^{\mathrm{2}} −\mathrm{4c}^{\mathrm{4}} + \\ $$$$\mathrm{12150}\pm\mathrm{108c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} \:}+\mathrm{729}+\mathrm{4c}^{\mathrm{4}} −\mathrm{784c}^{\mathrm{2}} +\mathrm{900c}^{\mathrm{2}} −\mathrm{4c}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{116c}^{\mathrm{2}} +\mathrm{63504}\pm\mathrm{1008c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{116c}^{\mathrm{2}} +\mathrm{63504}=\pm\mathrm{1008c}\sqrt{\mathrm{225}−\mathrm{c}^{\mathrm{2}} }\:. \\ $$$$\mathrm{Squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{above}\:\mathrm{eqs}.\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{13456c}^{\mathrm{4}} +\mathrm{14}\:\mathrm{732}\:\mathrm{928c}^{\mathrm{2}} +\mathrm{4}\:\mathrm{032}\:\mathrm{758}\:\mathrm{016}=\mathrm{1}\:\mathrm{016}\:\mathrm{064c}^{\mathrm{2}} \left(\mathrm{225}−\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{1}\:\mathrm{029}\:\mathrm{520c}^{\mathrm{4}} −\mathrm{213}\:\mathrm{881}\:\mathrm{472c}^{\mathrm{2}} +\mathrm{4}\:\mathrm{032}\:\mathrm{758}\:\mathrm{016}=\mathrm{0}\left(\mathrm{6}\right) \\ $$$$\mathrm{Solve}\:\left(\mathrm{6}\right)\:\mathrm{by}\:\mathrm{caculator}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{c}^{\mathrm{2}} \in\left\{\frac{\mathrm{15876}}{\mathrm{85}};\frac{\mathrm{15876}}{\mathrm{757}}\right\}\Rightarrow\mathrm{c}\in\left\{\pm\mathrm{13}.\mathrm{66661884},\pm\mathrm{4}.\mathrm{57954789}\right\} \\ $$$$\left.\boldsymbol{\mathrm{a}}\right)\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{c}}=\mathrm{13}.\mathrm{66661884}\:\mathrm{from}\:\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{b}\in\left\{\mathrm{19}.\mathrm{84913689},\mathrm{7}.\mathrm{484100795}\right\}.\mathrm{Replace} \\ $$$$\mathrm{into}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{a}\in\left\{\mathrm{15}.\mathrm{4020625},\mathrm{3}.\mathrm{03702641}\right\} \\ $$$$\boldsymbol{\mathrm{Check}}\:\boldsymbol{\mathrm{directly}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{see}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{triple}} \\ $$$$\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\right)=\left(\mathrm{3}.\mathrm{0370};\mathrm{7}.\mathrm{484};\mathrm{13}.\mathrm{6666}\right\}\boldsymbol{\mathrm{i}}\mathrm{s}\:\mathrm{accepted} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{c}}=\mathrm{4}.\mathrm{579547894},\mathrm{similarly}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\right)=\left(\mathrm{13}.\mathrm{22980};−\mathrm{9}.\mathrm{7042800};\mathrm{4}.\mathrm{5795}\right) \\ $$$$\left.\boldsymbol{\mathrm{c}}\right)\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{c}}=−\mathrm{13}.\mathrm{66661884}\:\mathrm{from}\:\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{b}\in\left\{−\mathrm{7}.\mathrm{484100795},−\mathrm{19}.\mathrm{84913689}\right\} \\ $$$$\mathrm{a}\in\left\{−\mathrm{3}.\mathrm{03702641},−\mathrm{15}.\mathrm{4020625}\right\} \\ $$$$\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\right)=\left(−\mathrm{3}.\mathrm{037},−\mathrm{7}.\mathrm{4841},−\mathrm{13}.\mathrm{6666}\right) \\ $$$$\left.\boldsymbol{\mathrm{d}}\right)\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{c}}=−\mathrm{4}.\mathrm{57954789}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{b}\in\left\{\mathrm{9}.\mathrm{704280069},−\mathrm{18}.\mathrm{86337585}\right\} \\ $$$$\mathrm{a}\in\left\{−\mathrm{13}.\mathrm{22980503},−\mathrm{41}.\mathrm{79746098}\right\} \\ $$$$\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\right)=\left(−\mathrm{13}.\mathrm{22980},\mathrm{9}.\mathrm{70428},−\mathrm{4}.\mathrm{5795}\right) \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\boldsymbol{\mathrm{four}}\:\boldsymbol{\mathrm{triples}}\:\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\right)\:\boldsymbol{\mathrm{satisfy}} \\ $$$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{system}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equtions}} \\ $$
Commented by I want to learn more last updated on 24/Jul/20
Wow, thanks sir. I appreciate.
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *