Menu Close

Solve-a-x-3-2-gt-5-b-3x-2-gt-12-

Tinku Tara 0 Comments
Pin




Question Number 80405 by TawaTawa last updated on 02/Feb/20
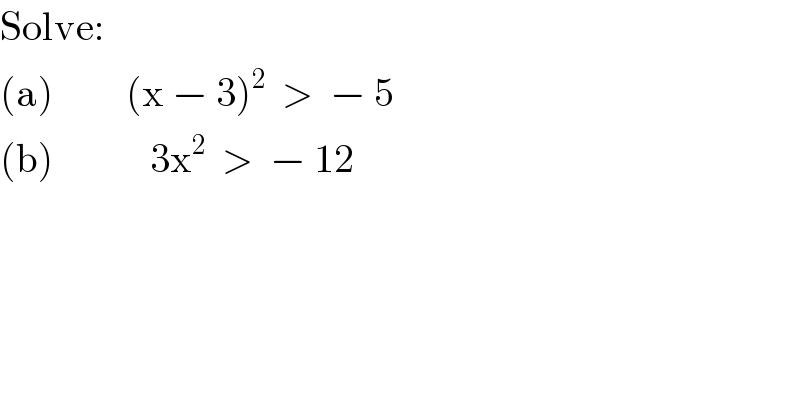
Solve: (a) (x − 3)^2 > − 5 (b) 3x^2 > − 12
$$\mathrm{Solve}: \\ $$$$\left(\mathrm{a}\right)\:\:\:\:\:\:\:\:\:\left(\mathrm{x}\:−\:\mathrm{3}\right)^{\mathrm{2}} \:\:>\:\:−\:\mathrm{5} \\ $$$$\left(\mathrm{b}\right)\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}^{\mathrm{2}} \:\:>\:\:−\:\mathrm{12} \\ $$
Commented by MJS last updated on 02/Feb/20
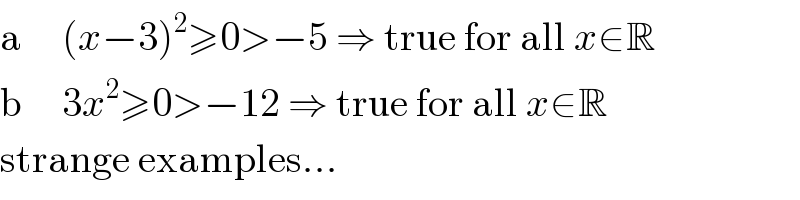
a (x−3)^2 ≥0>−5 ⇒ true for all x∈R b 3x^2 ≥0>−12 ⇒ true for all x∈R strange examples...
$$\mathrm{a}\:\:\:\:\:\left({x}−\mathrm{3}\right)^{\mathrm{2}} \geqslant\mathrm{0}>−\mathrm{5}\:\Rightarrow\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{x}\in\mathbb{R} \\ $$$$\mathrm{b}\:\:\:\:\:\mathrm{3}{x}^{\mathrm{2}} \geqslant\mathrm{0}>−\mathrm{12}\:\Rightarrow\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{x}\in\mathbb{R} \\ $$$$\mathrm{strange}\:\mathrm{examples}… \\ $$
Commented by TawaTawa last updated on 02/Feb/20
Sir, no workings ??
$$\mathrm{Sir},\:\:\mathrm{no}\:\mathrm{workings}\:?? \\ $$
Commented by MJS last updated on 02/Feb/20
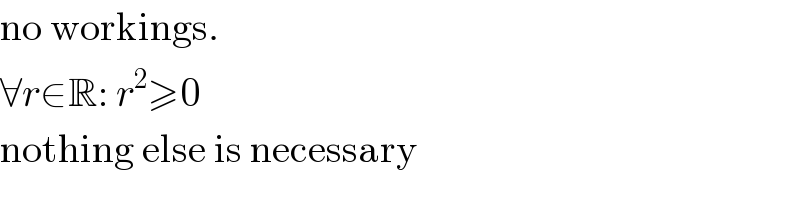
no workings. ∀r∈R: r^2 ≥0 nothing else is necessary
$$\mathrm{no}\:\mathrm{workings}. \\ $$$$\forall{r}\in\mathbb{R}:\:{r}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{nothing}\:\mathrm{else}\:\mathrm{is}\:\mathrm{necessary} \\ $$
Commented by TawaTawa last updated on 02/Feb/20
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by sandy_delta last updated on 03/Feb/20
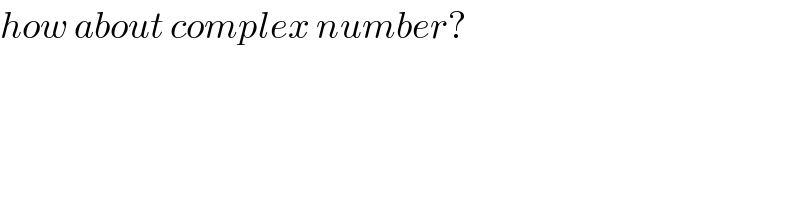
how about complex number?
$${how}\:{about}\:{complex}\:{number}? \\ $$
Commented by jagoll last updated on 03/Feb/20
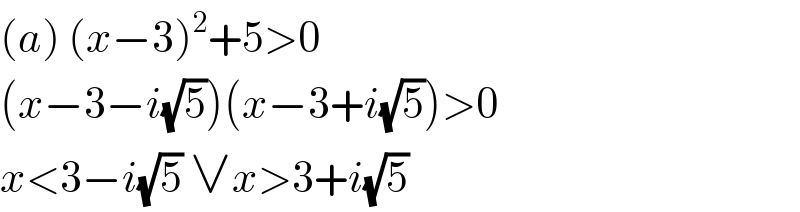
(a) (x−3)^2 +5>0 (x−3−i(√5))(x−3+i(√5))>0 x<3−i(√5) ∨x>3+i(√5)
$$\left({a}\right)\:\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{5}>\mathrm{0} \\ $$$$\left({x}−\mathrm{3}−{i}\sqrt{\mathrm{5}}\right)\left({x}−\mathrm{3}+{i}\sqrt{\mathrm{5}}\right)>\mathrm{0} \\ $$$${x}<\mathrm{3}−{i}\sqrt{\mathrm{5}}\:\vee{x}>\mathrm{3}+{i}\sqrt{\mathrm{5}} \\ $$
Commented by jagoll last updated on 03/Feb/20
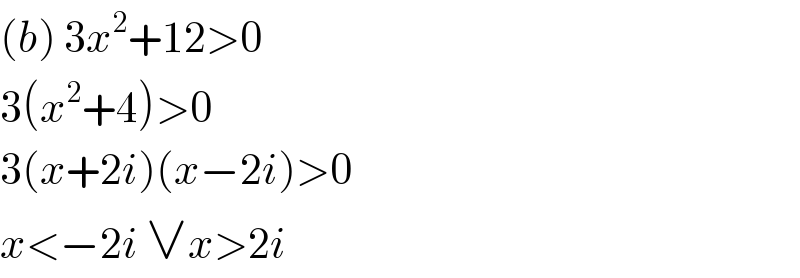
(b) 3x^2 +12>0 3(x^2 +4)>0 3(x+2i)(x−2i)>0 x<−2i ∨x>2i
$$\left({b}\right)\:\mathrm{3}{x}^{\mathrm{2}} +\mathrm{12}>\mathrm{0} \\ $$$$\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{4}\right)>\mathrm{0} \\ $$$$\mathrm{3}\left({x}+\mathrm{2}{i}\right)\left({x}−\mathrm{2}{i}\right)>\mathrm{0} \\ $$$${x}<−\mathrm{2}{i}\:\vee{x}>\mathrm{2}{i} \\ $$
Commented by MJS last updated on 03/Feb/20
complex numbers cannot be sorted using < or > so this makes no sense at all
$$\mathrm{complex}\:\mathrm{numbers}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{sorted}\:\mathrm{using} \\ $$$$<\:\mathrm{or}\:>\:\mathrm{so}\:\mathrm{this}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{sense}\:\mathrm{at}\:\mathrm{all} \\ $$
Commented by jagoll last updated on 03/Feb/20
−2i < 2i sir?
$$−\mathrm{2}{i}\:<\:\mathrm{2}{i}\:{sir}? \\ $$
Commented by MJS last updated on 03/Feb/20
−2i<2i ∣−2i −4i<0 ∣÷(−4) i>0 we are allowed to multiply both sides with a number>0 without changing the <> signs i>0 ∣×i i^2 >0 −1>0 wrong i<0??? we must change the <> signs when multiplying with a number <0 i<0 ∣×i i^2 >0 −1>0 wrong ⇒ i is neither >0 nor <0
$$−\mathrm{2i}<\mathrm{2i}\:\:\:\:\:\mid−\mathrm{2i} \\ $$$$−\mathrm{4i}<\mathrm{0}\:\:\:\:\:\mid\boldsymbol{\div}\left(−\mathrm{4}\right) \\ $$$$\mathrm{i}>\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{multiply}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{with} \\ $$$$\mathrm{a}\:\mathrm{number}>\mathrm{0}\:\mathrm{without}\:\mathrm{changing}\:\mathrm{the}\:<>\:\mathrm{signs} \\ $$$$\mathrm{i}>\mathrm{0}\:\:\:\:\:\mid×\mathrm{i} \\ $$$$\mathrm{i}^{\mathrm{2}} >\mathrm{0} \\ $$$$−\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{wrong} \\ $$$$ \\ $$$$\mathrm{i}<\mathrm{0}??? \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{change}\:\mathrm{the}\:<>\:\mathrm{signs}\:\mathrm{when}\:\mathrm{multiplying} \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{number}\:<\mathrm{0} \\ $$$$\mathrm{i}<\mathrm{0}\:\:\:\:\:\mid×\mathrm{i} \\ $$$$\mathrm{i}^{\mathrm{2}} >\mathrm{0} \\ $$$$−\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{wrong} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{i}\:{is}\:{neither}\:>\mathrm{0}\:{nor}\:<\mathrm{0} \\ $$
Commented by jagoll last updated on 03/Feb/20
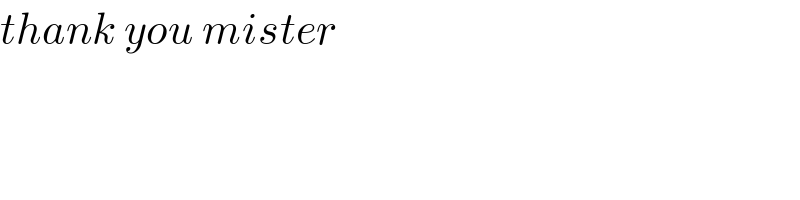
thank you mister
$${thank}\:{you}\:{mister} \\ $$
Answered by sandy_delta last updated on 03/Feb/20
(b) 3x^(2 ) > −12 x^2 > −4 x^2 − (−4) > 0 (x + (√(−4)))(x − (√(−4))) > 0 (x + 2i) (x−2i) > 0 x <−2i ∨ x>2i
$$\left({b}\right)\:\mathrm{3}{x}^{\mathrm{2}\:} >\:−\mathrm{12} \\ $$$${x}^{\mathrm{2}} \:>\:−\mathrm{4} \\ $$$${x}^{\mathrm{2}} \:−\:\left(−\mathrm{4}\right)\:>\:\mathrm{0} \\ $$$$\left({x}\:+\:\sqrt{−\mathrm{4}}\right)\left({x}\:−\:\sqrt{−\mathrm{4}}\right)\:>\:\mathrm{0} \\ $$$$\left({x}\:+\:\mathrm{2}{i}\right)\:\left({x}−\mathrm{2}{i}\right)\:>\:\mathrm{0} \\ $$$${x}\:<−\mathrm{2}{i}\:\vee\:{x}>\mathrm{2}{i} \\ $$
Commented by MJS last updated on 03/Feb/20
see my above comment and/or please tell me if −3i+5 is smaller or greater than −2i
$$\mathrm{see}\:\mathrm{my}\:\mathrm{above}\:\mathrm{comment}\:\mathrm{and}/\mathrm{or}\:\mathrm{please}\:\mathrm{tell} \\ $$$$\mathrm{me}\:\mathrm{if} \\ $$$$−\mathrm{3i}+\mathrm{5}\:\mathrm{is}\:\mathrm{smaller}\:\mathrm{or}\:\mathrm{greater}\:\mathrm{than}\:−\mathrm{2i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *