Question Number 106214 by john santu last updated on 03/Aug/20

$$\mathrm{solve}\::\:\mathrm{arc}\:\mathrm{cos}\:\left(\mathrm{x}−\mathrm{1}\right)=\:\mathrm{2arc}\:\mathrm{cos}\:\left(\mathrm{x}\right) \\ $$$$\mathrm{where}\:\mathrm{x}\:\mathrm{is}\:\mathrm{real}. \\ $$
Answered by bobhans last updated on 03/Aug/20
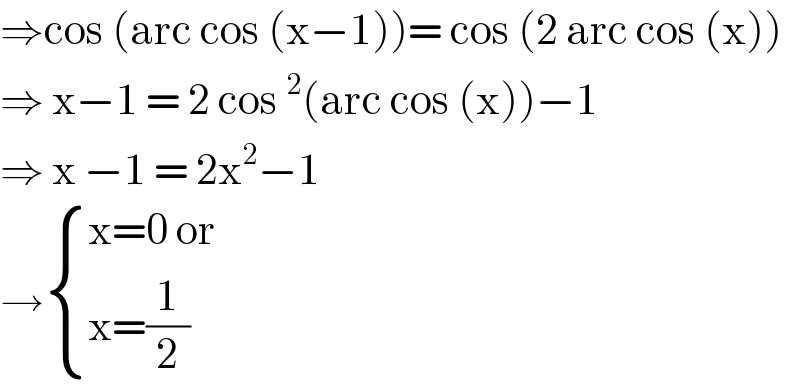
$$\Rightarrow\mathrm{cos}\:\left(\mathrm{arc}\:\mathrm{cos}\:\left(\mathrm{x}−\mathrm{1}\right)\right)=\:\mathrm{cos}\:\left(\mathrm{2}\:\mathrm{arc}\:\mathrm{cos}\:\left(\mathrm{x}\right)\right) \\ $$$$\Rightarrow\:\mathrm{x}−\mathrm{1}\:=\:\mathrm{2}\:\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{arc}\:\mathrm{cos}\:\left(\mathrm{x}\right)\right)−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}\:−\mathrm{1}\:=\:\mathrm{2x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\rightarrow\begin{cases}{\mathrm{x}=\mathrm{0}\:\mathrm{or}}\\{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$
