solve-by-simpson-s-rule-1-2-2-e-x-2-x-dx-

Question Number 96883 by M±th+et+s last updated on 05/Jun/20

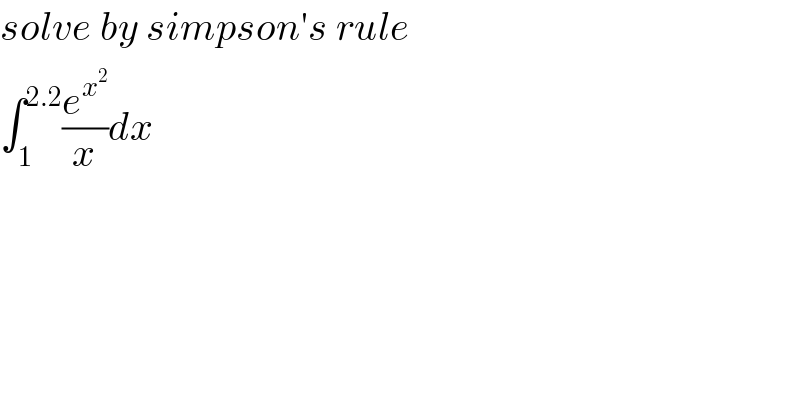
s o l v e b y {s i m p s o n}^{'} s r u l e

\int_{1}^{2.2} \frac{e^{x^{2}}}{x} d x

Commented by M±th+et+s last updated on 05/Jun/20

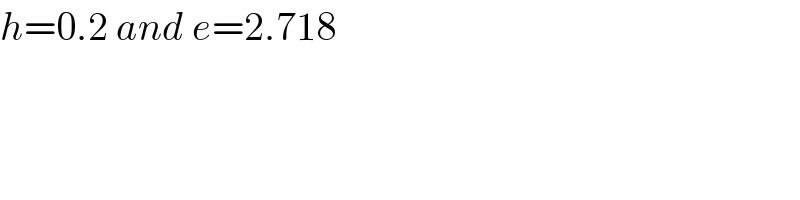
h = 0.2 a n d e = 2.718

Commented by PRITHWISH SEN 2 last updated on 05/Jun/20

x = 1, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2

I_{\frac{1}{3}} = \frac{h}{3} {(y_{0} + y_{6}) + 4 (y_{1} + y_{3} + y_{5}) + 2 (y_{2} + y_{4})}

= \frac{0.2}{3} {(2.718 + 57.457) + 4 (3.516 + 8.082 + 27.287)

+ 2 (5.069 + 14.180)} = 16.947