Question Number 61107 by arcana last updated on 29/May/19
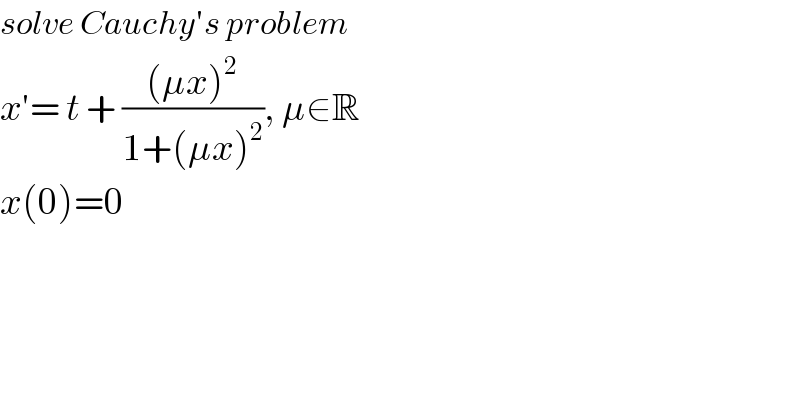
$${solve}\:{Cauchy}'{s}\:{problem} \\ $$$${x}'=\:{t}\:+\:\frac{\left(\mu{x}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\mu{x}\right)^{\mathrm{2}} },\:\mu\in\mathbb{R} \\ $$$${x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
