Solve-clairaut-s-equation-and-find-general-and-singular-solution-i-y-px-p-n-ii-y-1-p-xp-2-2-0-

Question Number 91812 by niroj last updated on 03/May/20

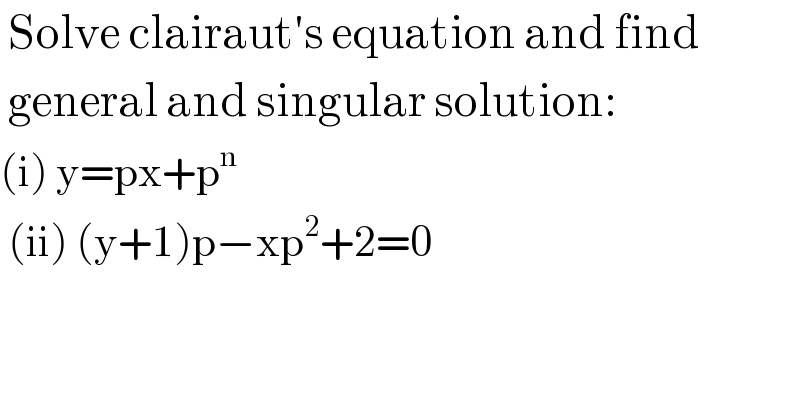
Solve {clairaut}^{'} s equation and find

general and singular solution :

(i) y = px + p^{n}

(ii) (y + 1) p - {xp}^{2} + 2 = 0

Commented by john santu last updated on 03/May/20

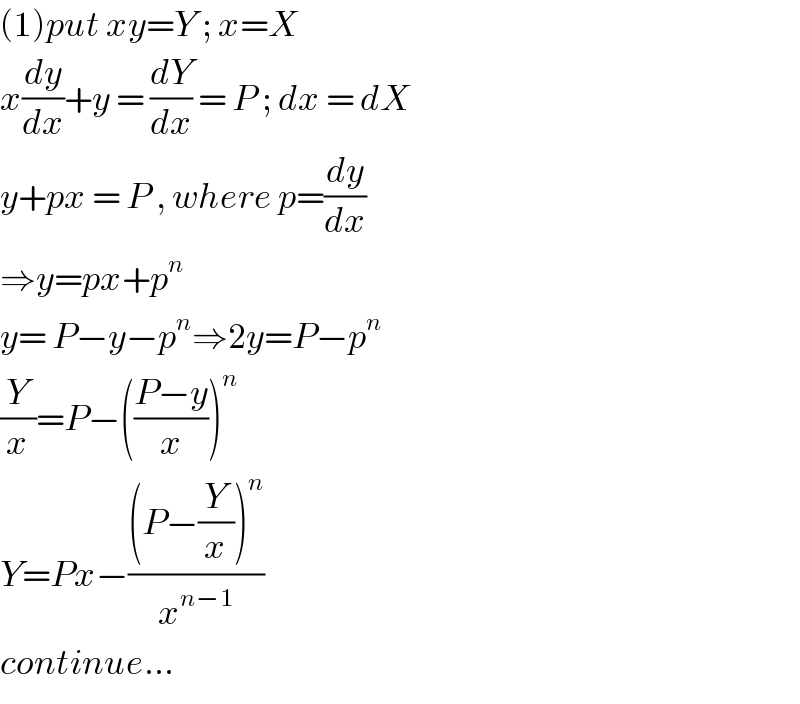
(1) p u t x y = Y; x = X

x \frac{d y}{d x} + y = \frac{d Y}{d x} = P; d x = d X

y + p x = P, w h e r e p = \frac{d y}{d x}

\Rightarrow y = p x + p^{n}

y = P - y - p^{n} \Rightarrow 2 y = P - p^{n}

\frac{Y}{x} = P - {(\frac{P - y}{x})}^{n}

Y = P x - \frac{{(P - \frac{Y}{x})}^{n}}{x^{n - 1}}

c o n t i n u e \dots

Commented by john santu last updated on 03/May/20

��