Question Number 106469 by ZiYangLee last updated on 05/Aug/20
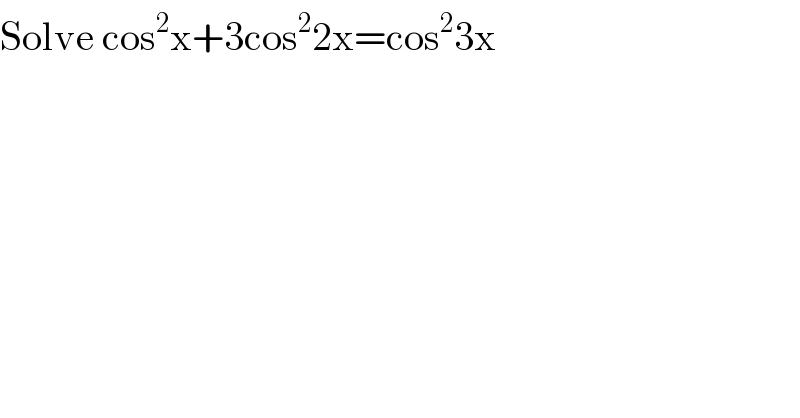
$$\mathrm{Solve}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{3cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{cos}^{\mathrm{2}} \mathrm{3x} \\ $$
Answered by mahdi last updated on 05/Aug/20
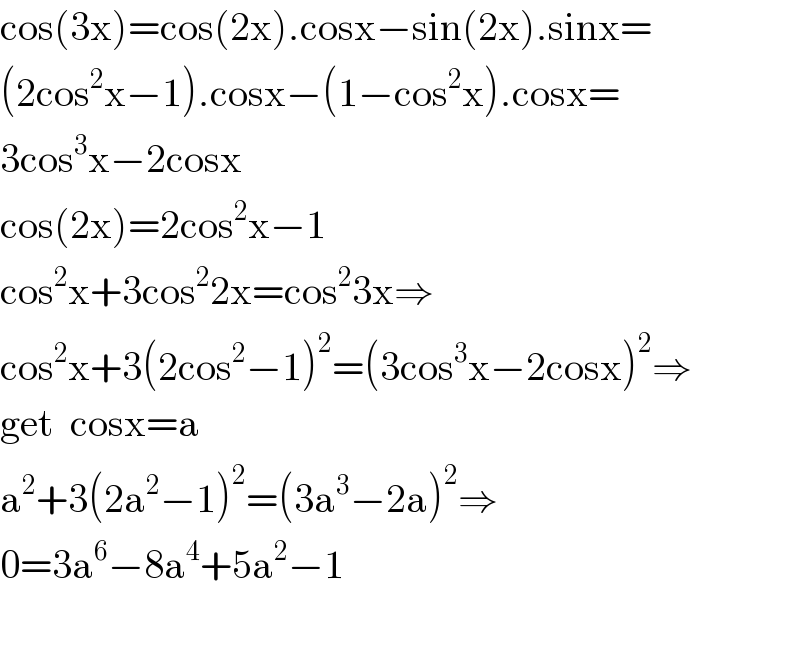
$$\mathrm{cos}\left(\mathrm{3x}\right)=\mathrm{cos}\left(\mathrm{2x}\right).\mathrm{cosx}−\mathrm{sin}\left(\mathrm{2x}\right).\mathrm{sinx}= \\ $$$$\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right).\mathrm{cosx}−\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right).\mathrm{cosx}= \\ $$$$\mathrm{3cos}^{\mathrm{3}} \mathrm{x}−\mathrm{2cosx} \\ $$$$\mathrm{cos}\left(\mathrm{2x}\right)=\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{3cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{cos}^{\mathrm{2}} \mathrm{3x}\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{3}\left(\mathrm{2cos}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{3cos}^{\mathrm{3}} \mathrm{x}−\mathrm{2cosx}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\mathrm{get}\:\:\mathrm{cosx}=\mathrm{a} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{3}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{3a}^{\mathrm{3}} −\mathrm{2a}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\mathrm{0}=\mathrm{3a}^{\mathrm{6}} −\mathrm{8a}^{\mathrm{4}} +\mathrm{5a}^{\mathrm{2}} −\mathrm{1} \\ $$$$ \\ $$
Commented by malwaan last updated on 06/Aug/20
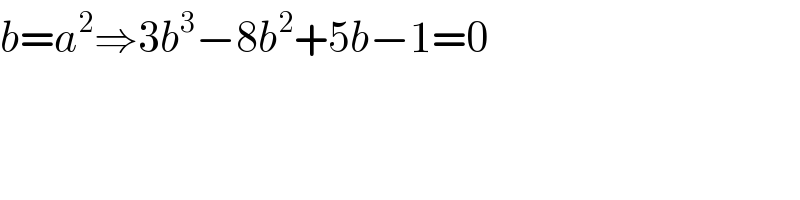
$${b}={a}^{\mathrm{2}} \Rightarrow\mathrm{3}{b}^{\mathrm{3}} −\mathrm{8}{b}^{\mathrm{2}} +\mathrm{5}{b}−\mathrm{1}=\mathrm{0} \\ $$
Answered by john santu last updated on 05/Aug/20
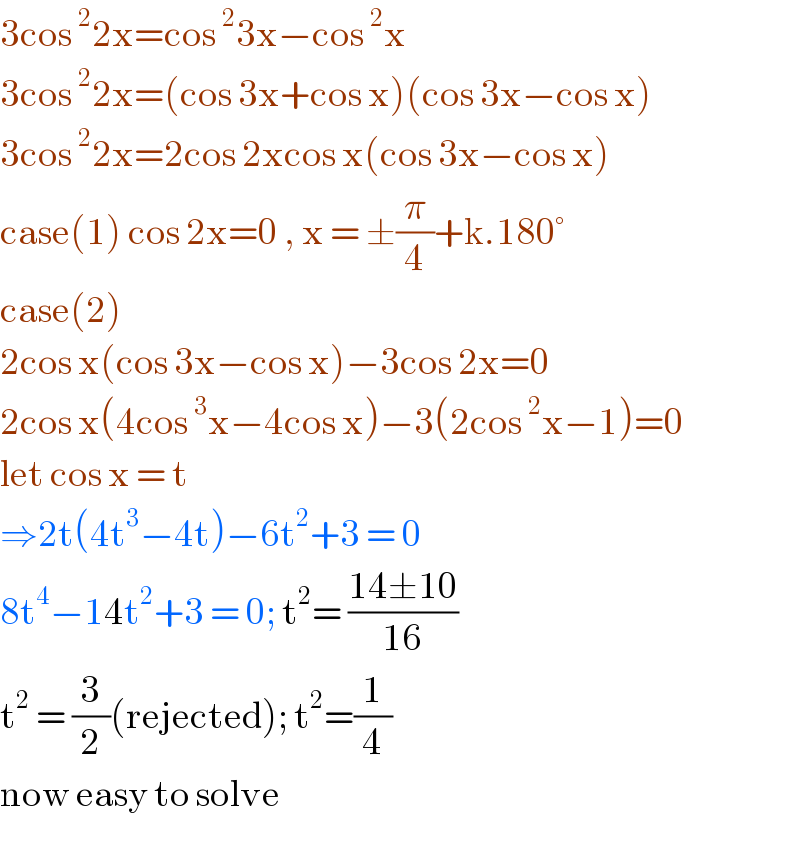
$$\mathrm{3cos}\:^{\mathrm{2}} \mathrm{2x}=\mathrm{cos}\:^{\mathrm{2}} \mathrm{3x}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{3cos}\:^{\mathrm{2}} \mathrm{2x}=\left(\mathrm{cos}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{x}\right)\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\mathrm{3cos}\:^{\mathrm{2}} \mathrm{2x}=\mathrm{2cos}\:\mathrm{2xcos}\:\mathrm{x}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{cos}\:\mathrm{2x}=\mathrm{0}\:,\:\mathrm{x}\:=\:\pm\frac{\pi}{\mathrm{4}}+\mathrm{k}.\mathrm{180}° \\ $$$$\mathrm{case}\left(\mathrm{2}\right) \\ $$$$\mathrm{2cos}\:\mathrm{x}\left(\mathrm{cos}\:\mathrm{3x}−\mathrm{cos}\:\mathrm{x}\right)−\mathrm{3cos}\:\mathrm{2x}=\mathrm{0} \\ $$$$\mathrm{2cos}\:\mathrm{x}\left(\mathrm{4cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{4cos}\:\mathrm{x}\right)−\mathrm{3}\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{t} \\ $$$$\Rightarrow\mathrm{2t}\left(\mathrm{4t}^{\mathrm{3}} −\mathrm{4t}\right)−\mathrm{6t}^{\mathrm{2}} +\mathrm{3}\:=\:\mathrm{0} \\ $$$$\mathrm{8t}^{\mathrm{4}} −\mathrm{14t}^{\mathrm{2}} +\mathrm{3}\:=\:\mathrm{0};\:\mathrm{t}^{\mathrm{2}} =\:\frac{\mathrm{14}\pm\mathrm{10}}{\mathrm{16}} \\ $$$$\mathrm{t}^{\mathrm{2}} \:=\:\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{rejected}\right);\:\mathrm{t}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{now}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by ZiYangLee last updated on 05/Aug/20

$$\mathrm{thank}\:\mathrm{you}\:<\mathrm{33} \\ $$
Commented by john santu last updated on 05/Aug/20

$$\geqslant\mathrm{44}.\: \\ $$
