Question Number 164671 by mnjuly1970 last updated on 20/Jan/22
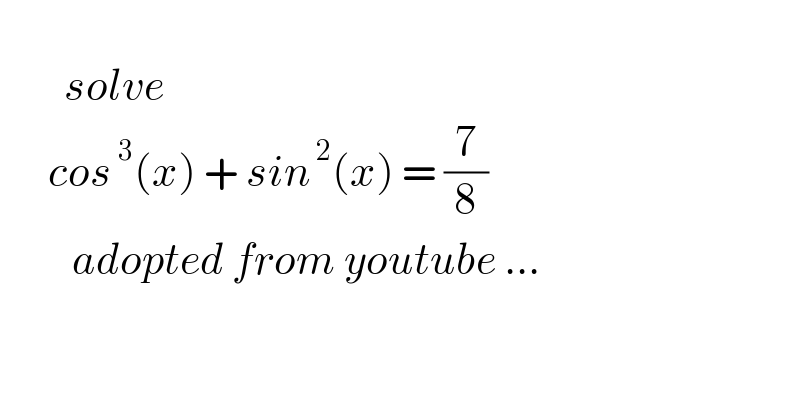
$$ \\ $$$$\:\:\:\:\:\:\:\:{solve}\: \\ $$$$\:\:\:\:\:\:{cos}^{\:\mathrm{3}} \left({x}\right)\:+\:{sin}^{\:\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{7}}{\mathrm{8}}\: \\ $$$$\:\:\:\:\:\:\:\:\:{adopted}\:{from}\:{youtube}\:… \\ $$$$ \\ $$
Commented by MJS_new last updated on 20/Jan/22
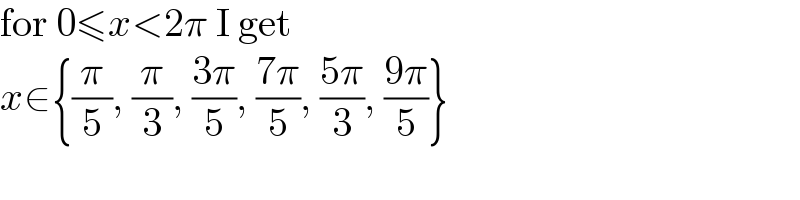
$$\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\mathrm{I}\:\mathrm{get} \\ $$$${x}\in\left\{\frac{\pi}{\mathrm{5}},\:\frac{\pi}{\mathrm{3}},\:\frac{\mathrm{3}\pi}{\mathrm{5}},\:\frac{\mathrm{7}\pi}{\mathrm{5}},\:\frac{\mathrm{5}\pi}{\mathrm{3}},\:\frac{\mathrm{9}\pi}{\mathrm{5}}\right\} \\ $$
Answered by bobhans last updated on 20/Jan/22
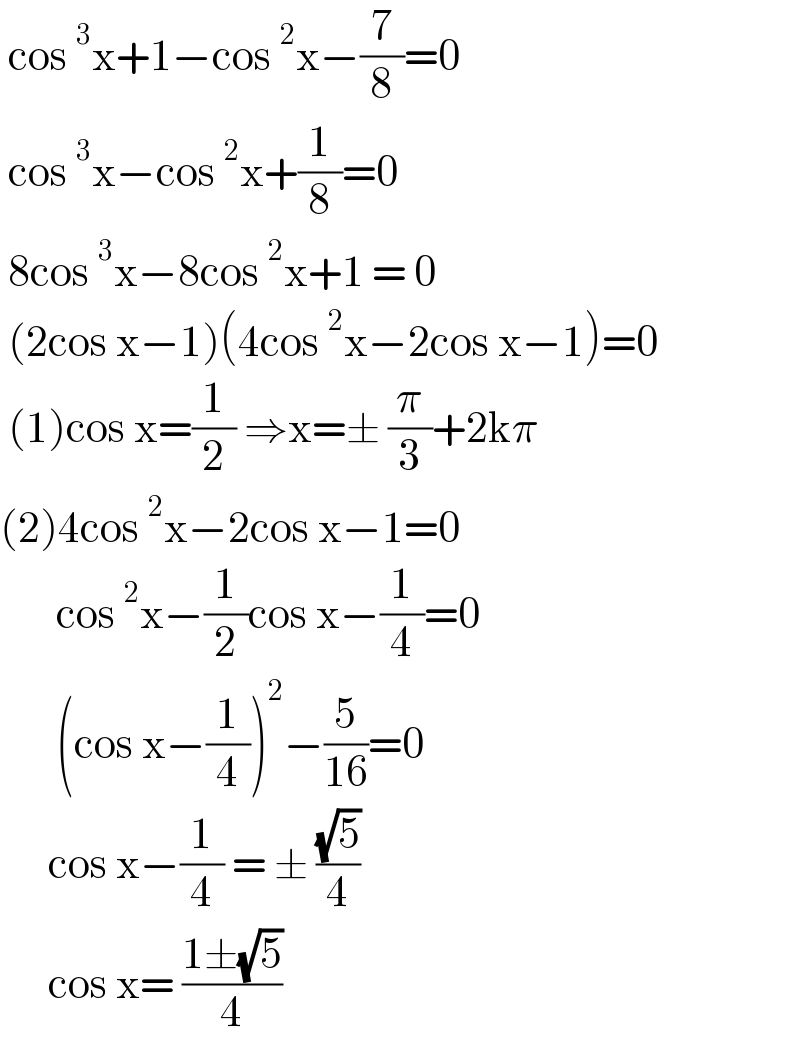
$$\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}+\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{7}}{\mathrm{8}}=\mathrm{0}\: \\ $$$$\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$$\:\mathrm{8cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{8cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\left(\mathrm{2cos}\:\mathrm{x}−\mathrm{1}\right)\left(\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{2cos}\:\mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\left(\mathrm{1}\right)\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{x}=\pm\:\frac{\pi}{\mathrm{3}}+\mathrm{2k}\pi \\ $$$$\left(\mathrm{2}\right)\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{2cos}\:\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{16}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}\:=\:\pm\:\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\mathrm{cos}\:\mathrm{x}=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}}\:\: \\ $$
