Question Number 88491 by M±th+et£s last updated on 11/Apr/20

$$\boldsymbol{{solve}} \\ $$$${cos}\left({x}\right)={k} \\ $$
Answered by mr W last updated on 11/Apr/20
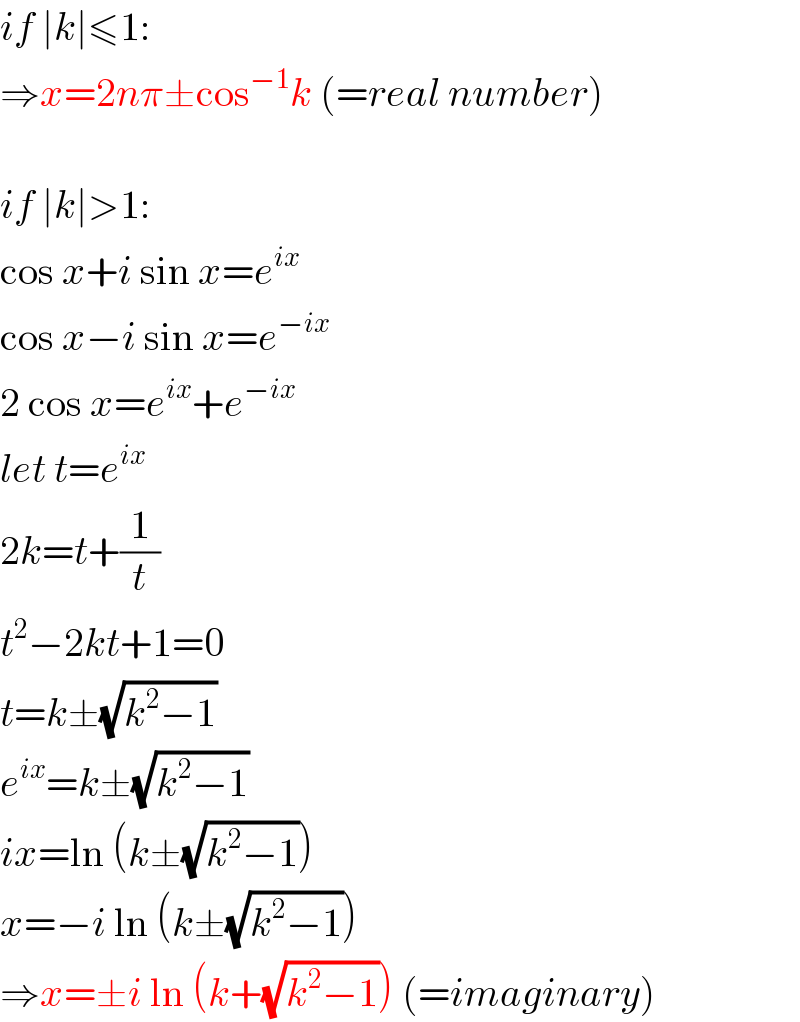
$${if}\:\mid{k}\mid\leqslant\mathrm{1}: \\ $$$$\Rightarrow{x}=\mathrm{2}{n}\pi\pm\mathrm{cos}^{−\mathrm{1}} {k}\:\left(={real}\:{number}\right) \\ $$$$ \\ $$$${if}\:\mid{k}\mid>\mathrm{1}: \\ $$$$\mathrm{cos}\:{x}+{i}\:\mathrm{sin}\:{x}={e}^{{ix}} \\ $$$$\mathrm{cos}\:{x}−{i}\:\mathrm{sin}\:{x}={e}^{−{ix}} \\ $$$$\mathrm{2}\:\mathrm{cos}\:{x}={e}^{{ix}} +{e}^{−{ix}} \\ $$$${let}\:{t}={e}^{{ix}} \\ $$$$\mathrm{2}{k}={t}+\frac{\mathrm{1}}{{t}} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{kt}+\mathrm{1}=\mathrm{0} \\ $$$${t}={k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$${e}^{{ix}} ={k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$${ix}=\mathrm{ln}\:\left({k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$${x}=−{i}\:\mathrm{ln}\:\left({k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow{x}=\pm{i}\:\mathrm{ln}\:\left({k}+\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\right)\:\left(={imaginary}\right) \\ $$
Commented by M±th+et£s last updated on 11/Apr/20
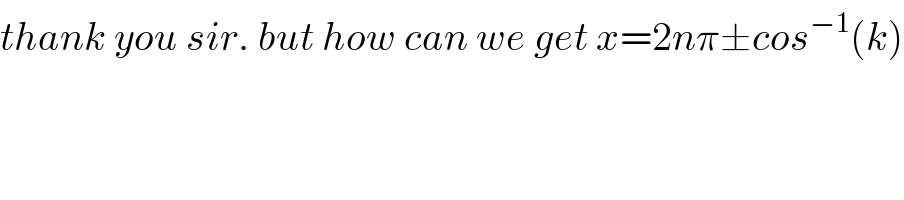
$${thank}\:{you}\:{sir}.\:{but}\:{how}\:{can}\:{we}\:{get}\:{x}=\mathrm{2}{n}\pi\pm{cos}^{−\mathrm{1}} \left({k}\right) \\ $$
Commented by Kunal12588 last updated on 11/Apr/20
![genral solution of cos x = m ; m∈[−1,1] is x=2nπ±cos^(−1) m ; n∈Z](https://www.tinkutara.com/question/Q88531.png)
$${genral}\:{solution}\:{of} \\ $$$${cos}\:{x}\:=\:{m}\:;\:{m}\in\left[−\mathrm{1},\mathrm{1}\right]\:\:\:\:{is}\: \\ $$$${x}=\mathrm{2}{n}\pi\pm{cos}^{−\mathrm{1}} {m}\:;\:\:{n}\in\mathbb{Z} \\ $$
