Question Number 162512 by vishal1234 last updated on 30/Dec/21
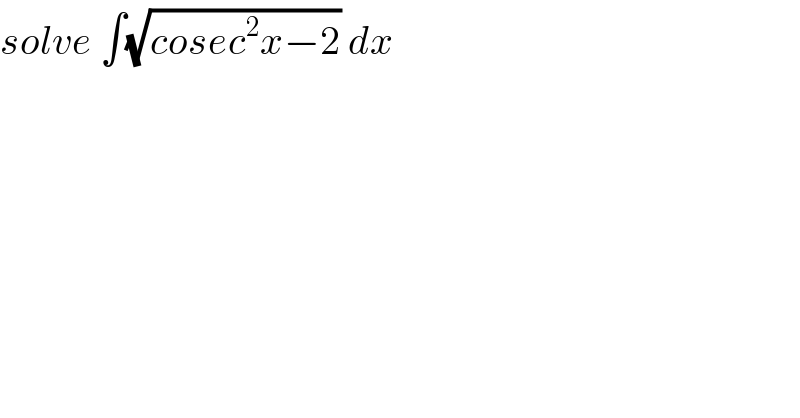
$${solve}\:\int\sqrt{{cosec}^{\mathrm{2}} {x}−\mathrm{2}}\:{dx} \\ $$
Commented by MJS_new last updated on 30/Dec/21
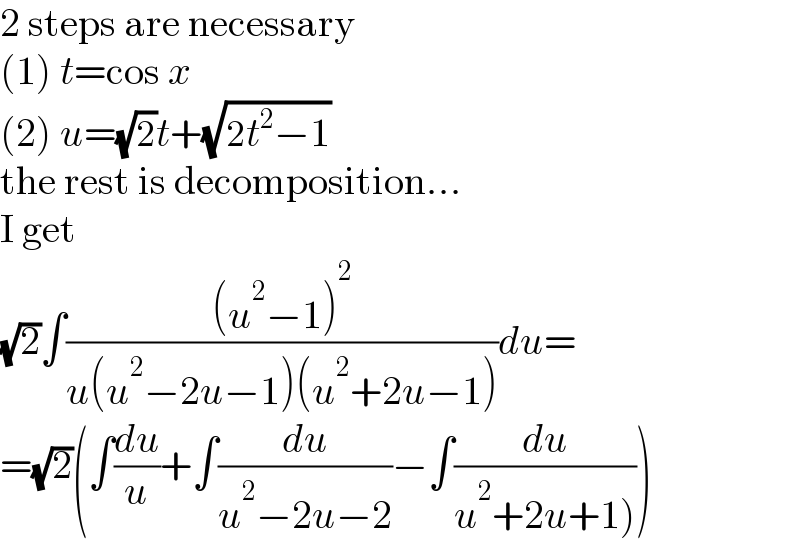
$$\mathrm{2}\:\mathrm{steps}\:\mathrm{are}\:\mathrm{necessary} \\ $$$$\left(\mathrm{1}\right)\:{t}=\mathrm{cos}\:{x} \\ $$$$\left(\mathrm{2}\right)\:{u}=\sqrt{\mathrm{2}}{t}+\sqrt{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{decomposition}… \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{2}}\int\frac{\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{u}\left({u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}\right)}{du}= \\ $$$$=\sqrt{\mathrm{2}}\left(\int\frac{{du}}{{u}}+\int\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{2}}−\int\frac{{du}}{\left.{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{1}\right)}\right) \\ $$
