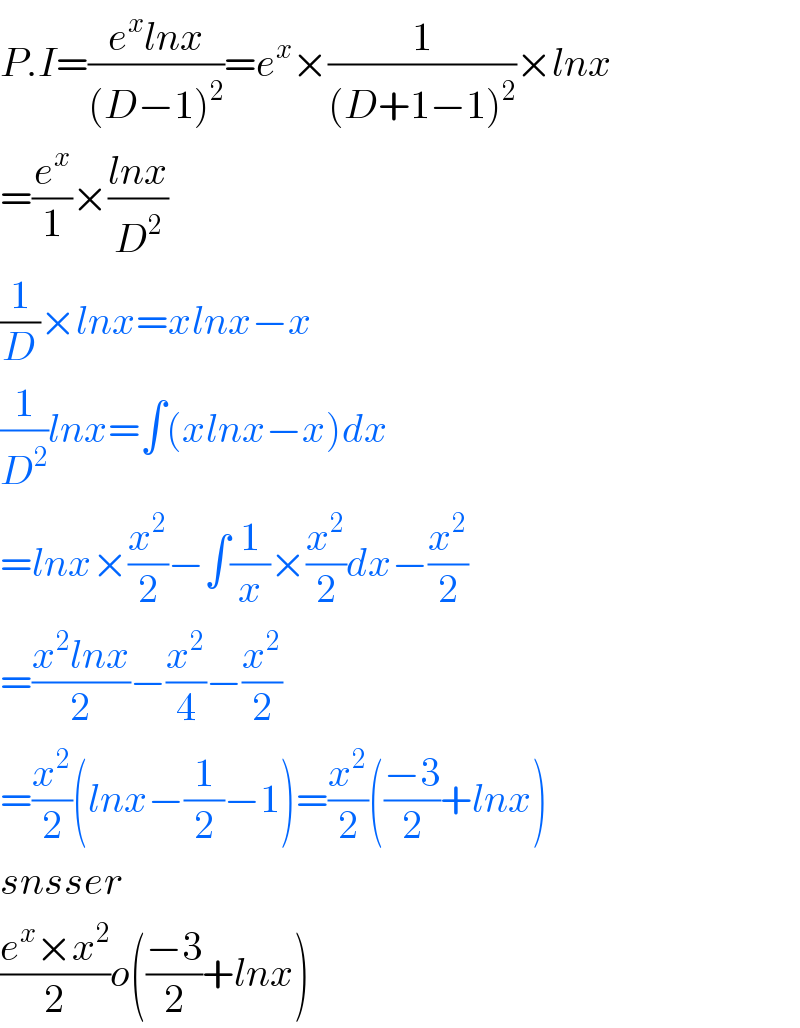solve-D-2-2D-1-y-e-x-ln-x-by-using-the-method-of-variation-of-parameters-

Question Number 119065 by benjo_mathlover last updated on 21/Oct/20

s o l v e (D^{2} - 2 D + 1) y = e^{x} \ln x

b y u s i n g t h e m e t h o d o f v a r i a t i o n

o f p a r a m e t e r s .

Answered by Olaf last updated on 22/Oct/20

y = e^{x} u

y^{'} = (u^{'} + u) e^{x}

y^{″} = (u^{″} + 2 u^{'} + u) e^{x}

u^{″} + 2 u^{'} + u - 2 (u^{'} + u) + u = \ln x

u^{″} = \ln x

u^{'} = \int \ln x d x = x \ln x - x + C_{1}

u = \int (x \ln x - x + C_{1}) d x

u = \frac{x^{2}}{2} \ln x - \int \frac{x^{2}}{2} . \frac{1}{x} d x - \frac{x^{2}}{2} + C_{1} x + C_{2}

u = \frac{x^{2}}{2} \ln x - \frac{x^{2}}{4} - \frac{x^{2}}{2} + C_{1} x + C_{2}

u = \frac{x^{2}}{2} \ln x - \frac{3 x^{2}}{4} + C_{1} x + C_{2}

y = (\frac{x^{2}}{2} \ln x - \frac{3 x^{2}}{4} + C_{1} x + C_{2}) e^{x}

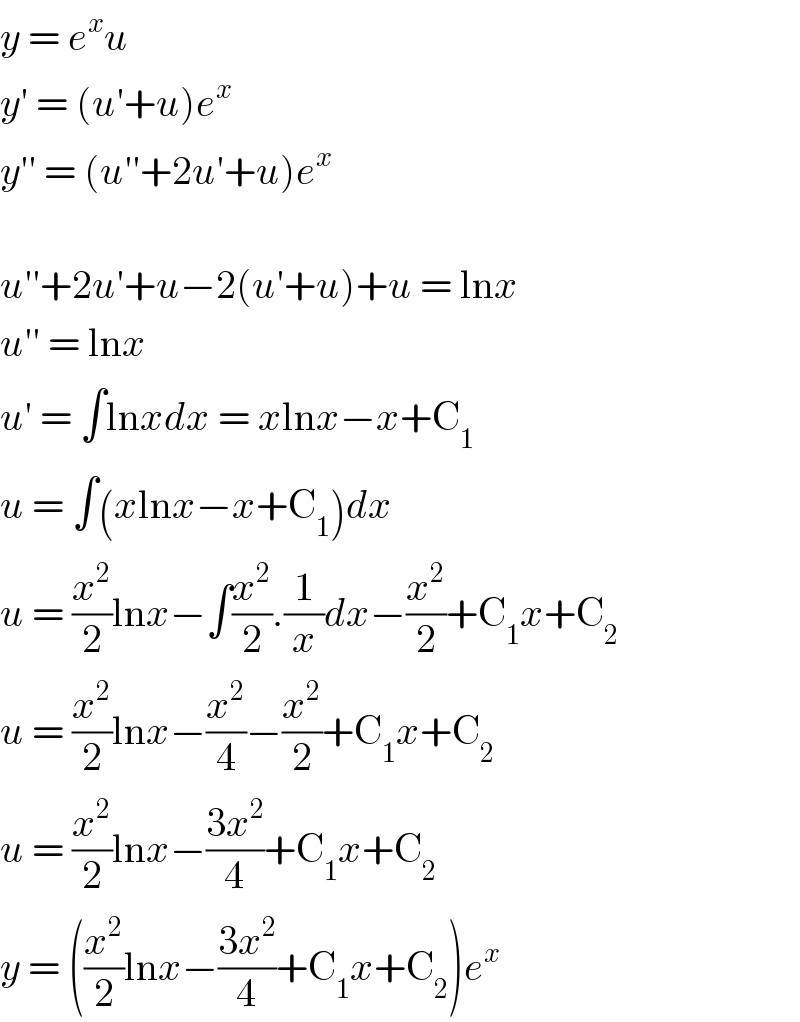
Commented by benjo_mathlover last updated on 22/Oct/20

t h a n k y o u

Answered by john santu last updated on 27/Oct/20

F o r t h e h o m o g e n o u s s o l u t i o n w e s o l v e t h e

c h a r a c t e r i s t i c e q u a t i o n

λ^{2} - 2 λ + 1 = 0, w h i c h h a s a d o u b l e r o o t λ = 1

h e n c e t h e h o m o g e n o u s s o l u t i o n c a n b e

w r i t t e n a s y_{h} = (C_{1} + C_{2} x) e^{x}

u s i n g t h e h o m o g e n o u s s o l u t i o n w e

c a n n o w b e g i n u s i n g v a r i a t i o n o f

p a r a m e t e r s m e t h o d

l e t y_{p} = u . e^{x} + v . {x e}^{x}

D i f f e r e n t i a t i n g y i e l d s

y^{'} = ({u e}^{x} + u^{'} e^{x}) + (v . (x + 1) e^{x} + v^{'} . {x e}^{x})

s e t u^{'} e^{x} + v^{'} {x e}^{x} = 0 o r u^{'} + {x v}^{'} = 0

w e g e t y^{'} = {u e}^{x} + v . (x + 1) e^{x}

D i f f e r e n t i a t i n g a g a i n g i v e s

y^{″} = {u e}^{x} + u^{'} e^{x} + v (x + 2) e^{x} + v^{'} (x + 1) e^{x}

s u b s t i t u t i n g i n t o t h e o r i g i n a l

d i f f e r e n t i a l e q u a t i o n

({u e}^{x} + u^{'} e^{x} + v (x + 2) e^{x} + v^{'} (x + 1) e^{x}) -

2 ({u e}^{x} + v (x + 1) e^{x}) + ({u e}^{x} + v . {x e}^{x}) = e^{x} . \ln x

t h i s r e d u c e s t o

u^{'} + (x + 1) v^{'} = \ln x

n o w w e h a v e t w o e q u a t i o n i n u^{'} a n d v^{'}

{\begin{cases} u^{'} + {x v}^{'} = 0 \\ u^{'} + (x + 1) v^{'} = \ln x \end{cases}

(\begin{matrix} 1 x \\ 1 x + 1 \end{matrix}) (\begin{matrix} u^{'} \\ v^{'} \end{matrix}) = (\begin{matrix} 0 \\ \ln x \end{matrix})

\to {\begin{cases} u^{'} = - x \ln x \\ v^{'} = \ln x \end{cases}

i n t e g r a t i n g w i t h b y p a r t s g i v e s

{\begin{cases} u = - \frac{1}{2} x^{2} \ln x + \frac{1}{4} x^{2} \\ v = x \ln x - x \end{cases}

t h u s p a r t i c u l a r s o l u t i o n e q u a l t o

y_{p} = - \frac{1}{2} x^{2} e^{x} \ln x + \frac{1}{4} x^{2} e^{x}

+ x^{2} e^{x} \ln x - x^{2} e^{x}

y_{p} = \frac{1}{2} x^{2} e^{x} \ln x - \frac{3}{4} x^{2} e^{x}

T h e r e f o r e w e c o n c l u d e t h a t a g e n e r a l

s o l u t i o n y = y_{h} + y_{p}

y = (C_{1} + C_{2} x) e^{x} + \frac{1}{4} (2 \ln x - 3) x^{2} e^{x}

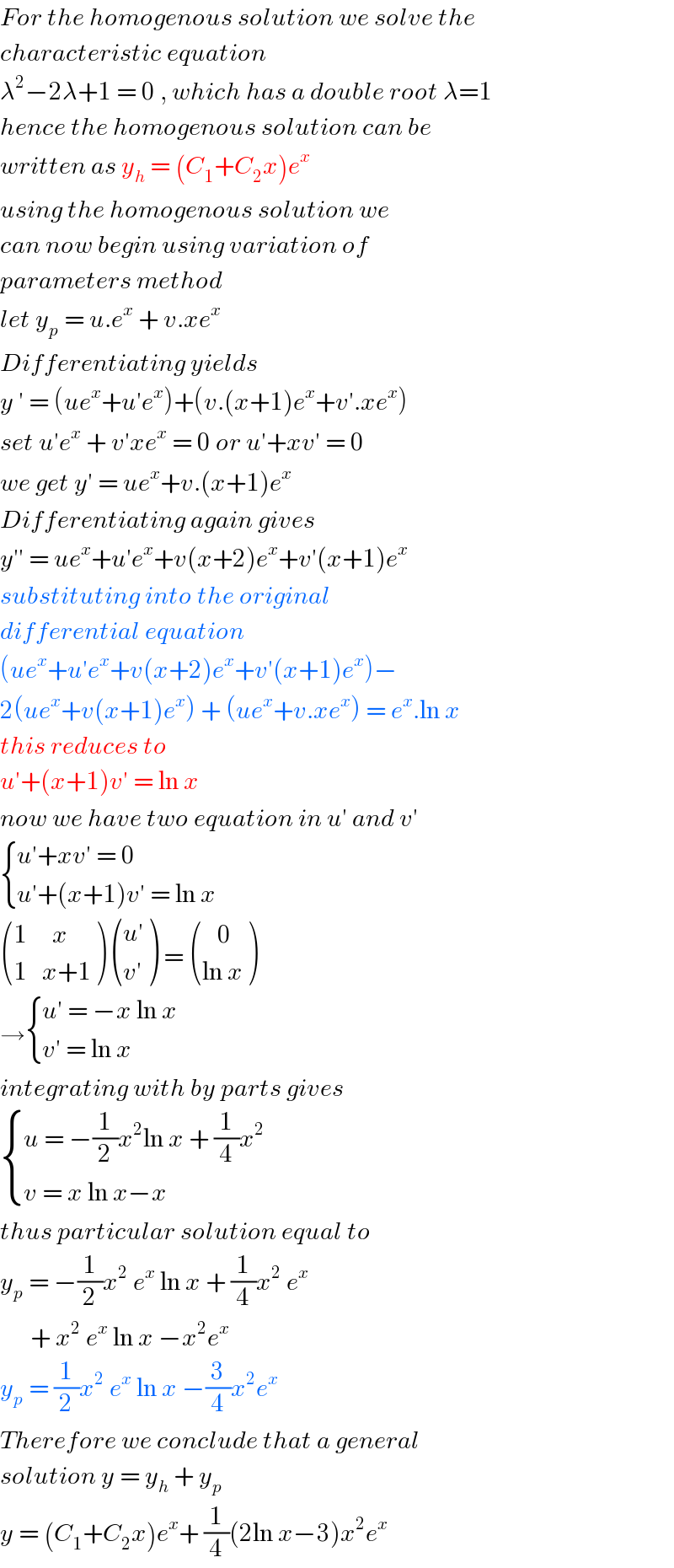
Answered by TANMAY PANACEA last updated on 22/Oct/20

P . I = \frac{e^{x} l n x}{{(D - 1)}^{2}} = e^{x} \times \frac{1}{{(D + 1 - 1)}^{2}} \times l n x

= \frac{e^{x}}{1} \times \frac{l n x}{D^{2}}

\frac{1}{D} \times l n x = x l n x - x

\frac{1}{D^{2}} l n x = \int (x l n x - x) d x

= l n x \times \frac{x^{2}}{2} - \int \frac{1}{x} \times \frac{x^{2}}{2} d x - \frac{x^{2}}{2}

= \frac{x^{2} l n x}{2} - \frac{x^{2}}{4} - \frac{x^{2}}{2}

= \frac{x^{2}}{2} (l n x - \frac{1}{2} - 1) = \frac{x^{2}}{2} (\frac{- 3}{2} + l n x)

s n s s e r

\frac{e^{x} \times x^{2}}{2} o (\frac{- 3}{2} + l n x)