Menu Close

solve-D-2-a-y-tan-ax-

Tinku Tara 0 Comments
Pin




Question Number 126683 by bramlexs22 last updated on 23/Dec/20
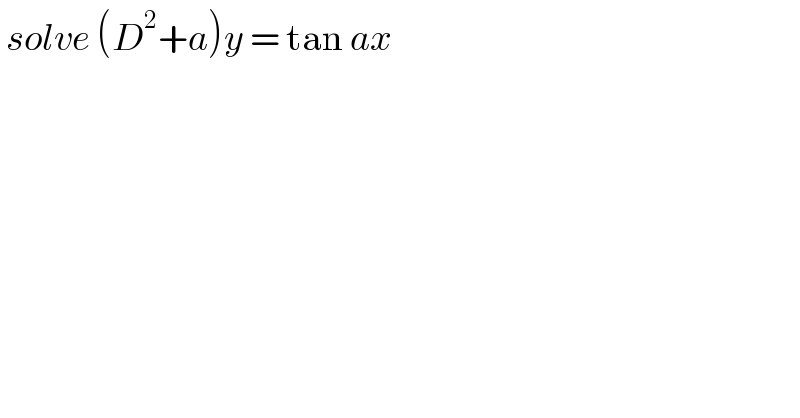
solve (D^2 +a)y = tan ax
$$\:{solve}\:\left({D}^{\mathrm{2}} +{a}\right){y}\:=\:\mathrm{tan}\:{ax}\: \\ $$
Answered by liberty last updated on 23/Dec/20
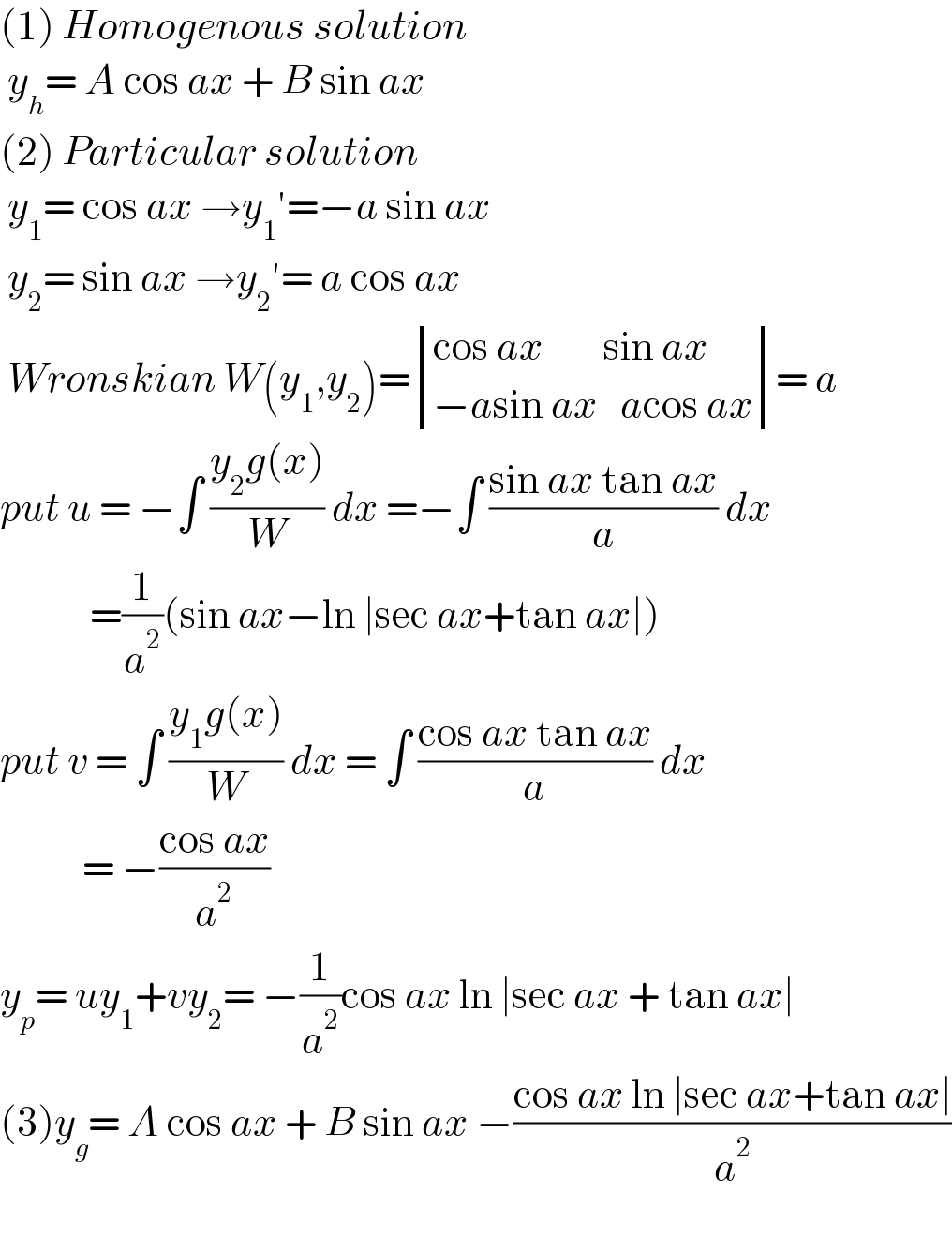
(1) Homogenous solution y_h = A cos ax + B sin ax (2) Particular solution y_1 = cos ax →y_1 ′=−a sin ax y_2 = sin ax →y_2 ′= a cos ax Wronskian W(y_1 ,y_2 )= determinant (((cos ax sin ax)),((−asin ax acos ax)))= a put u = −∫ ((y_2 g(x))/W) dx =−∫ ((sin ax tan ax)/a) dx =(1/a^2 )(sin ax−ln ∣sec ax+tan ax∣) put v = ∫ ((y_1 g(x))/W) dx = ∫ ((cos ax tan ax)/a) dx = −((cos ax)/a^2 ) y_p = uy_1 +vy_2 = −(1/a^2 )cos ax ln ∣sec ax + tan ax∣ (3)y_g = A cos ax + B sin ax −((cos ax ln ∣sec ax+tan ax∣)/a^2 )
$$\left(\mathrm{1}\right)\:{Homogenous}\:{solution} \\ $$$$\:{y}_{{h}} =\:{A}\:\mathrm{cos}\:{ax}\:+\:{B}\:\mathrm{sin}\:{ax}\: \\ $$$$\left(\mathrm{2}\right)\:{Particular}\:{solution}\: \\ $$$$\:{y}_{\mathrm{1}} =\:\mathrm{cos}\:{ax}\:\rightarrow{y}_{\mathrm{1}} '=−{a}\:\mathrm{sin}\:{ax} \\ $$$$\:{y}_{\mathrm{2}} =\:\mathrm{sin}\:{ax}\:\rightarrow{y}_{\mathrm{2}} '=\:{a}\:\mathrm{cos}\:{ax} \\ $$$$\:{Wronskian}\:{W}\left({y}_{\mathrm{1}} ,{y}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{cos}\:{ax}\:\:\:\:\:\:\:\:\mathrm{sin}\:{ax}}\\{−{a}\mathrm{sin}\:{ax}\:\:\:{a}\mathrm{cos}\:{ax}}\end{vmatrix}=\:{a} \\ $$$${put}\:{u}\:=\:−\int\:\frac{{y}_{\mathrm{2}} {g}\left({x}\right)}{{W}}\:{dx}\:=−\int\:\frac{\mathrm{sin}\:{ax}\:\mathrm{tan}\:{ax}}{{a}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left(\mathrm{sin}\:{ax}−\mathrm{ln}\:\mid\mathrm{sec}\:{ax}+\mathrm{tan}\:{ax}\mid\right) \\ $$$${put}\:{v}\:=\:\int\:\frac{{y}_{\mathrm{1}} {g}\left({x}\right)}{{W}}\:{dx}\:=\:\int\:\frac{\mathrm{cos}\:{ax}\:\mathrm{tan}\:{ax}}{{a}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{cos}\:{ax}}{{a}^{\mathrm{2}} } \\ $$$${y}_{{p}} =\:{uy}_{\mathrm{1}} +{vy}_{\mathrm{2}} =\:−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\mathrm{cos}\:{ax}\:\mathrm{ln}\:\mid\mathrm{sec}\:{ax}\:+\:\mathrm{tan}\:{ax}\mid \\ $$$$\left(\mathrm{3}\right){y}_{{g}} =\:{A}\:\mathrm{cos}\:{ax}\:+\:{B}\:\mathrm{sin}\:{ax}\:−\frac{\mathrm{cos}\:{ax}\:\mathrm{ln}\:\mid\mathrm{sec}\:{ax}+\mathrm{tan}\:{ax}\mid}{{a}^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 24/Dec/20
y^(′′) +ay =tanx h→r^2 +a=0 case 1 a>0 ⇒r^2 =−a ⇒r=+^− (√(−a))=+^− i(√a) ⇒ y_h =ae^(i(√a)x) +be^(−i(√a)x) =αcos((√a)x)+βsin((√a)x)=αu_1 +βu_2 w(u_1 ,u_2 )= determinant (((cos((√a)x) sin((√a)x))),((−(√a)sin((√a)x) (√a)cos((√a)x))))=(√a) w_1 = determinant (((o sin((√a)x))),((tan(ax) (√a)cos((√a)x))))=−sin((√a)x)tan(ax)) w_2 = determinant (((cos((√a)x) 0)),((−(√a)sin((√a)x) tan(ax))))=cos((√a)x)tan(ax) v_1 =∫ (w_1 /w)dx =−∫ ((sin((√a)x)tan(ax))/( (√a)))dx =−(1/( (√a)))∫ sin((√a)x)tan(ax)dx v_2 =∫ (w_2 /w)dx =∫ ((cos((√a)x)tan(ax))/( (√a)))dx ⇒y_p =u_1 v_1 +u_2 v_2 =−(1/( (√a)))cos((√a)x)∫ sin((√a)x)tan(ax)dx +(1/( (√a)))sin((√a)x)∫ cos((√a)x)tan(ax)dx ⇒ general solution is y =y_p +h_h case 2 <0 r^2 +a=0 ⇒r^2 =−a ⇒r=+^− (√a) ⇒ y_h =a e^((√a)x) +be^(−(√a)x) =au_1 +bu_2 and we follow the same way...
$$\mathrm{y}^{''} \:+\mathrm{ay}\:=\mathrm{tanx} \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{a}=\mathrm{0} \\ $$$$\mathrm{case}\:\mathrm{1}\:\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} \:=−\mathrm{a}\:\Rightarrow\mathrm{r}=\overset{−} {+}\sqrt{−\mathrm{a}}=\overset{−} {+}\mathrm{i}\sqrt{\mathrm{a}}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{i}\sqrt{\mathrm{a}}\mathrm{x}} \:+\mathrm{be}^{−\mathrm{i}\sqrt{\mathrm{a}}\mathrm{x}} \:=\alpha\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)+\beta\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{w}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\:\:\:\:\:\:\:\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)}\\{−\sqrt{\mathrm{a}}\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\:\:\:\:\sqrt{\mathrm{a}}\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)}\end{vmatrix}=\sqrt{\mathrm{a}} \\ $$$$\left.\mathrm{w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)}\\{\mathrm{tan}\left(\mathrm{ax}\right)\:\:\:\sqrt{\mathrm{a}}\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)}\end{vmatrix}=−\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)\right) \\ $$$$\mathrm{w}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\sqrt{\mathrm{a}}\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\:\:\mathrm{tan}\left(\mathrm{ax}\right)}\end{vmatrix}=\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\frac{\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)}{\:\sqrt{\mathrm{a}}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\int\:\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)}{\:\sqrt{\mathrm{a}}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\int\:\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)\mathrm{dx} \\ $$$$+\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}\mathrm{sin}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\int\:\:\mathrm{cos}\left(\sqrt{\mathrm{a}}\mathrm{x}\right)\mathrm{tan}\left(\mathrm{ax}\right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{p}} \:+\mathrm{h}_{\mathrm{h}} \\ $$$$\mathrm{case}\:\mathrm{2}\:\:<\mathrm{0}\:\:\mathrm{r}^{\mathrm{2}} \:+\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} \:=−\mathrm{a}\:\Rightarrow\mathrm{r}=\overset{−} {+}\sqrt{\mathrm{a}}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\sqrt{\mathrm{a}}\mathrm{x}} \:+\mathrm{be}^{−\sqrt{\mathrm{a}}\mathrm{x}} \:\:\:\:\:\:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \:\:\mathrm{and}\:\mathrm{we}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *