solve-d-2-x-dt-2-cosx-

Question Number 144930 by alcohol last updated on 30/Jun/21

s o l v e

\frac{d^{2} x}{{d t}^{2}} = c o s x

Answered by ArielVyny last updated on 30/Jun/21

- c o s x

Answered by mr W last updated on 01/Jul/21

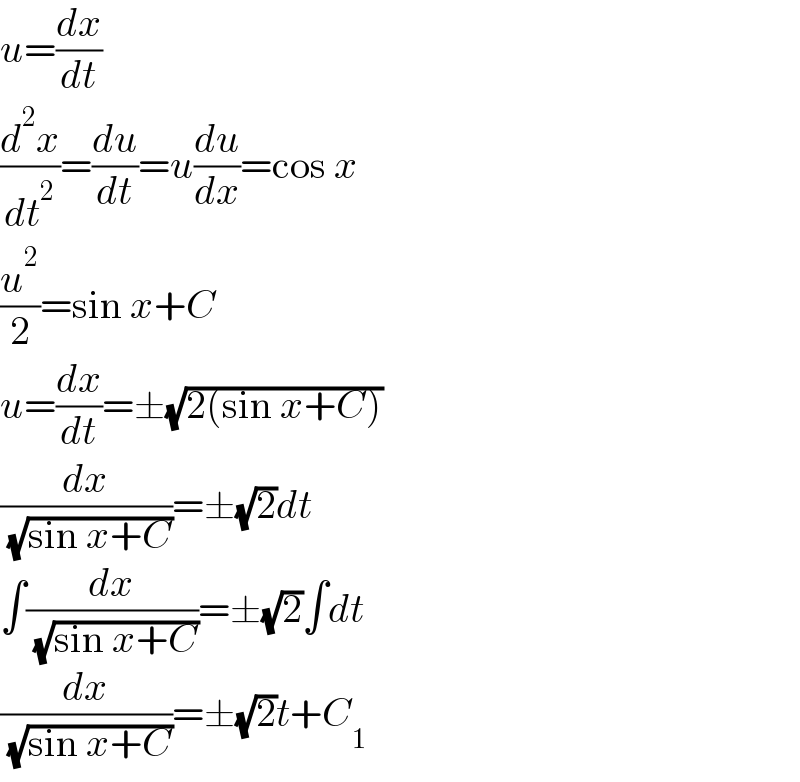
u = \frac{d x}{d t}

\frac{d^{2} x}{{d t}^{2}} = \frac{d u}{d t} = u \frac{d u}{d x} = \cos x

\frac{u^{2}}{2} = \sin x + C

u = \frac{d x}{d t} = \pm \sqrt{2 (\sin x + C)}

\frac{d x}{\sqrt{\sin x + C}} = \pm \sqrt{2} d t

\int \frac{d x}{\sqrt{\sin x + C}} = \pm \sqrt{2} \int d t

\frac{d x}{\sqrt{\sin x + C}} = \pm \sqrt{2} t + C_{1}

Facebook Tweet Pin