Question Number 40322 by rahul 19 last updated on 19/Jul/18
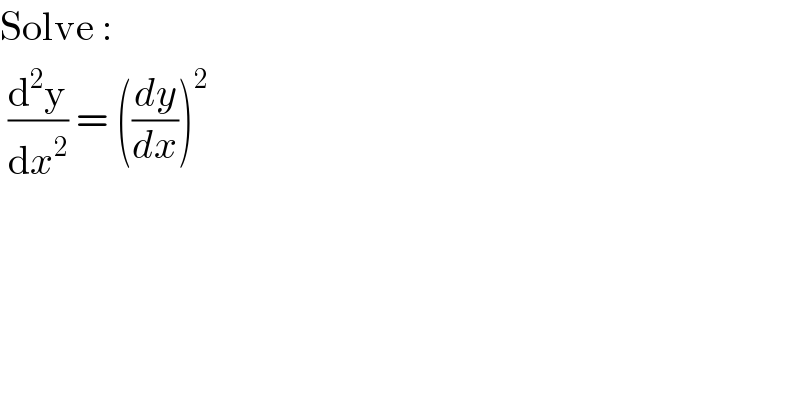
$$\mathrm{Solve}\:: \\ $$$$\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{d}{x}^{\mathrm{2}} }\:=\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 19/Jul/18
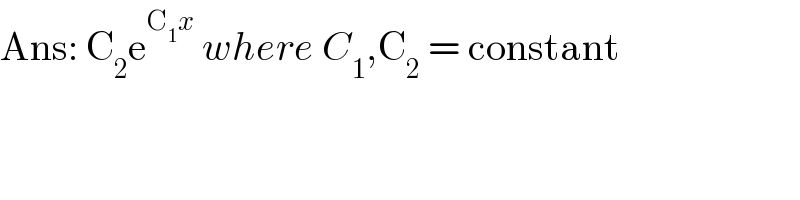
$$\mathrm{Ans}:\:\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{C}_{\mathrm{1}} {x}} \:{where}\:{C}_{\mathrm{1}} ,\mathrm{C}_{\mathrm{2}} \:=\:\mathrm{constant} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jul/18
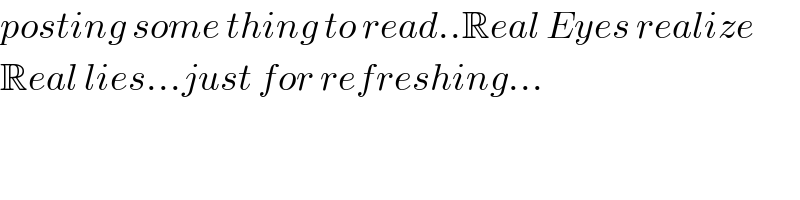
$${posting}\:{some}\:{thing}\:{to}\:{read}..\mathbb{R}{eal}\:{Eyes}\:{realize} \\ $$$$\mathbb{R}{eal}\:{lies}…{just}\:{for}\:{refreshing}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jul/18

Commented by rahul 19 last updated on 19/Jul/18
oh! ������������
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jul/18
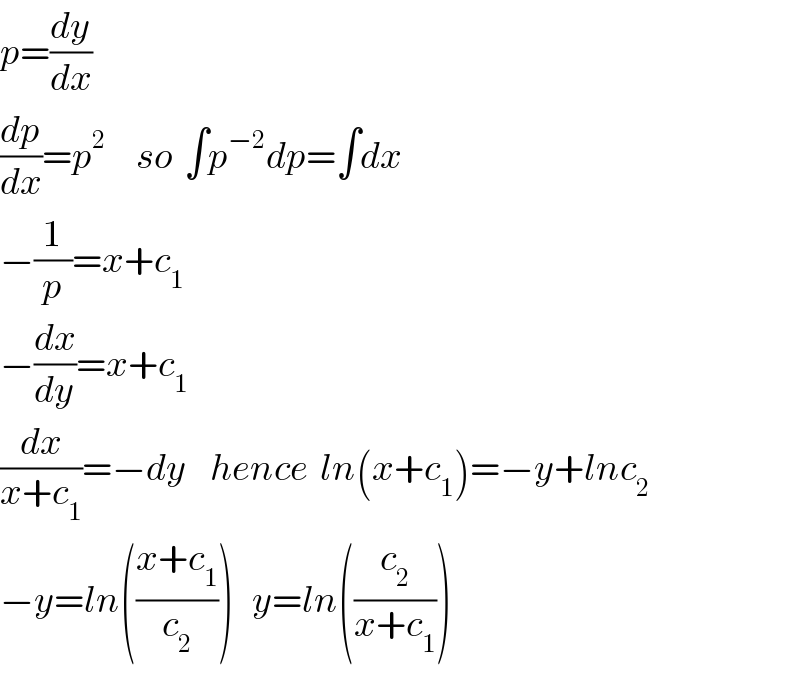
$${p}=\frac{{dy}}{{dx}} \\ $$$$\frac{{dp}}{{dx}}={p}^{\mathrm{2}} \:\:\:\:\:{so}\:\:\int{p}^{−\mathrm{2}} {dp}=\int{dx} \\ $$$$−\frac{\mathrm{1}}{{p}}={x}+{c}_{\mathrm{1}} \\ $$$$−\frac{{dx}}{{dy}}={x}+{c}_{\mathrm{1}} \\ $$$$\frac{{dx}}{{x}+{c}_{\mathrm{1}} }=−{dy}\:\:\:\:{hence}\:\:{ln}\left({x}+{c}_{\mathrm{1}} \right)=−{y}+{lnc}_{\mathrm{2}} \\ $$$$−{y}={ln}\left(\frac{{x}+{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} }\right)\:\:\:{y}={ln}\left(\frac{{c}_{\mathrm{2}} }{{x}+{c}_{\mathrm{1}} }\right) \\ $$
Commented by rahul 19 last updated on 19/Jul/18

$$\mathrm{Ans}.\:\mathrm{given}\:\mathrm{in}\:\mathrm{book}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct},\:\mathrm{right}? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jul/18
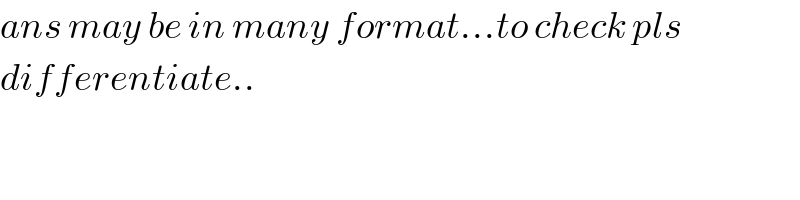
$${ans}\:{may}\:{be}\:{in}\:{many}\:{format}…{to}\:{check}\:{pls} \\ $$$${differentiate}.. \\ $$
