Question Number 90952 by jagoll last updated on 27/Apr/20
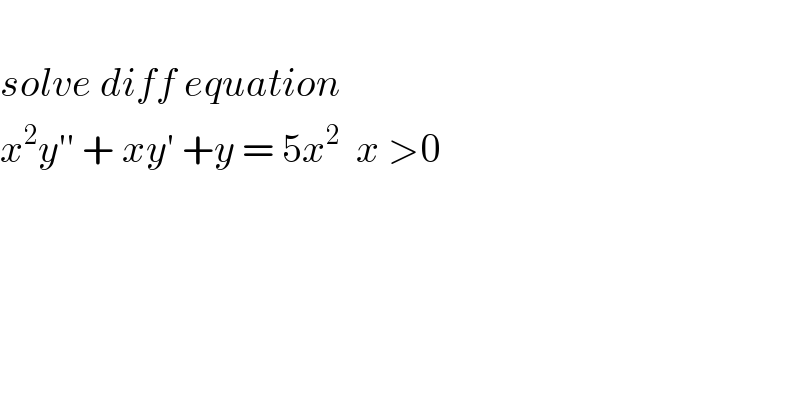
$$ \\ $$$${solve}\:{diff}\:{equation}\: \\ $$$${x}^{\mathrm{2}} {y}''\:+\:{xy}'\:+{y}\:=\:\mathrm{5}{x}^{\mathrm{2}} \:\:{x}\:>\mathrm{0} \\ $$
Answered by MWSuSon last updated on 27/Apr/20
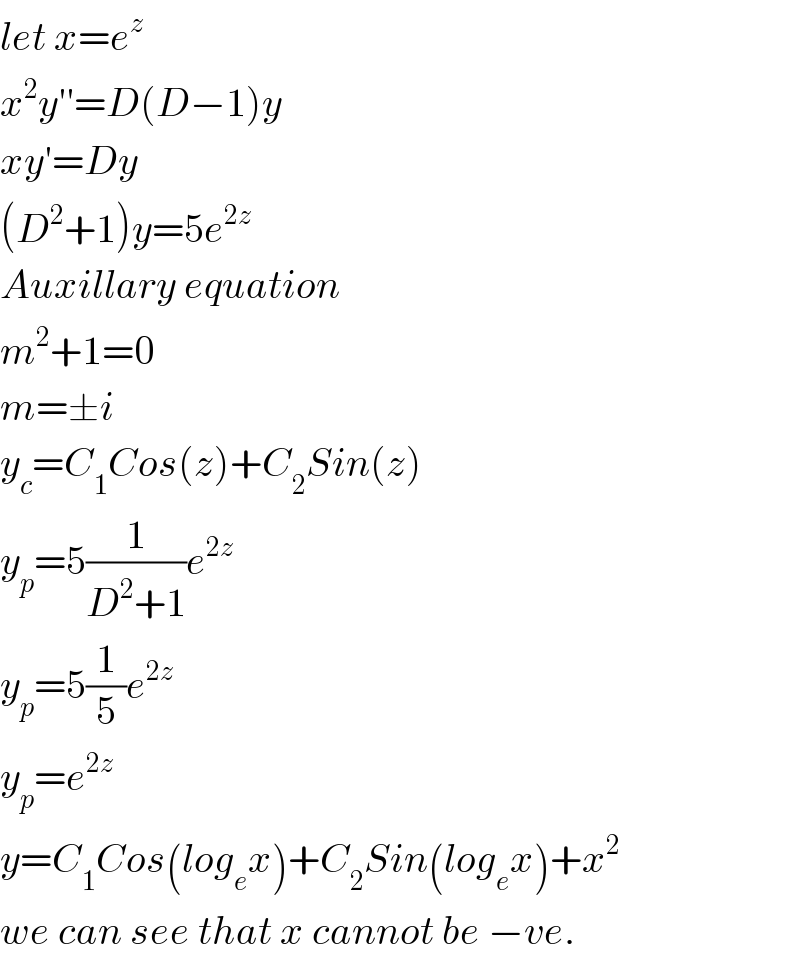
$${let}\:{x}={e}^{{z}} \\ $$$${x}^{\mathrm{2}} {y}''={D}\left({D}−\mathrm{1}\right){y} \\ $$$${xy}'={Dy} \\ $$$$\left({D}^{\mathrm{2}} +\mathrm{1}\right){y}=\mathrm{5}{e}^{\mathrm{2}{z}} \\ $$$${Auxillary}\:{equation} \\ $$$${m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${m}=\pm{i} \\ $$$${y}_{{c}} ={C}_{\mathrm{1}} {Cos}\left({z}\right)+{C}_{\mathrm{2}} {Sin}\left({z}\right) \\ $$$${y}_{{p}} =\mathrm{5}\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{1}}{e}^{\mathrm{2}{z}} \\ $$$${y}_{{p}} =\mathrm{5}\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{2}{z}} \\ $$$${y}_{{p}} ={e}^{\mathrm{2}{z}} \\ $$$${y}={C}_{\mathrm{1}} {Cos}\left({log}_{{e}} {x}\right)+{C}_{\mathrm{2}} {Sin}\left({log}_{{e}} {x}\right)+{x}^{\mathrm{2}} \\ $$$${we}\:{can}\:{see}\:{that}\:{x}\:{cannot}\:{be}\:−{ve}. \\ $$
Commented by jagoll last updated on 27/Apr/20
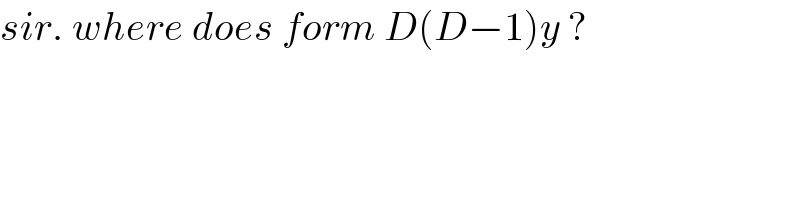
$${sir}.\:{where}\:{does}\:{form}\:{D}\left({D}−\mathrm{1}\right){y}\:? \\ $$
Commented by MWSuSon last updated on 27/Apr/20
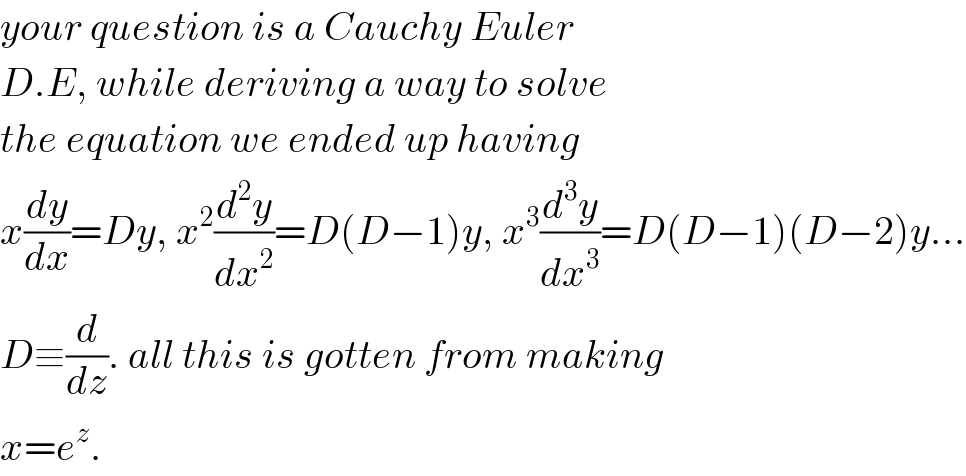
$${your}\:{question}\:{is}\:{a}\:{Cauchy}\:{Euler}\: \\ $$$${D}.{E},\:{while}\:{deriving}\:{a}\:{way}\:{to}\:{solve} \\ $$$${the}\:{equation}\:{we}\:{ended}\:{up}\:{having} \\ $$$${x}\frac{{dy}}{{dx}}={Dy},\:{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={D}\left({D}−\mathrm{1}\right){y},\:{x}^{\mathrm{3}} \frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }={D}\left({D}−\mathrm{1}\right)\left({D}−\mathrm{2}\right){y}… \\ $$$${D}\equiv\frac{{d}}{{dz}}.\:{all}\:{this}\:{is}\:{gotten}\:{from}\:{making} \\ $$$${x}={e}^{{z}} . \\ $$
Commented by jagoll last updated on 27/Apr/20
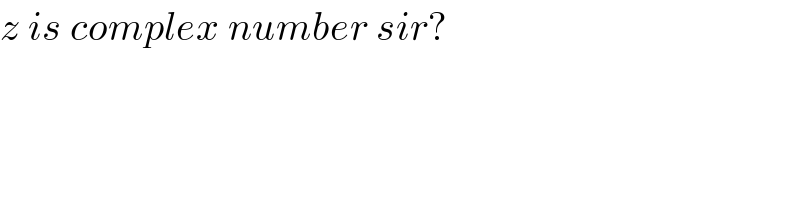
$${z}\:{is}\:{complex}\:{number}\:{sir}? \\ $$
Commented by MWSuSon last updated on 27/Apr/20
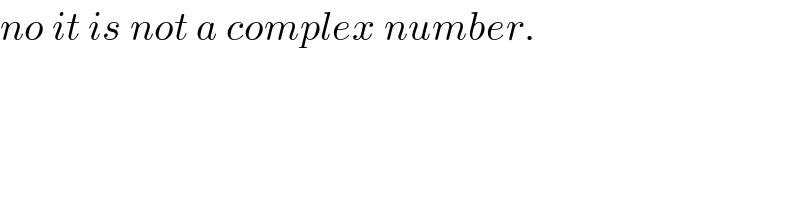
$${no}\:{it}\:{is}\:{not}\:{a}\:{complex}\:{number}. \\ $$
