solve-dx-3-5sin-x-

Question Number 118338 by benjo_mathlover last updated on 17/Oct/20

s o l v e \int \frac{d x}{3 - 5 \sin x}

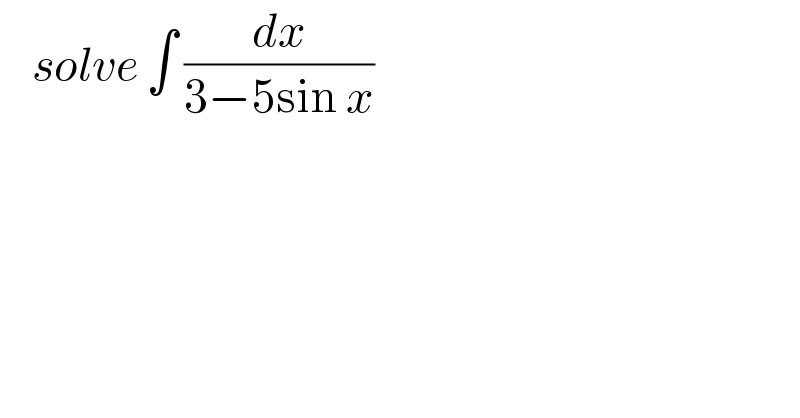
Answered by Dwaipayan Shikari last updated on 17/Oct/20

\int \frac{d x}{3 - 5 s i n x}

= 2 \int \frac{d t}{3 - \frac{10 t}{(1 + t^{2})}} . \frac{1}{1 + t^{2}} t = t a n \frac{x}{2}

= 2 \int \frac{d t}{3 + 3 t^{2} - 10 t} = \frac{2}{3} \int \frac{d t}{{(t - \frac{5}{3})}^{2} + 1 - \frac{25}{9}}

= \frac{2}{3} \int \frac{d t}{{(t - \frac{5}{3})}^{2} - {(\frac{4}{3})}^{2}}

= \frac{1}{4} l o g (\frac{t - \frac{5}{3} - \frac{4}{3}}{t - \frac{5}{3} + \frac{4}{3}}) = \frac{1}{4} l o g (\frac{3 t - 9}{3 t - 1}) = \frac{1}{4} l o g (\frac{3 t a n \frac{x}{2} - 9}{3 t a n \frac{x}{2} - 1}) + 4

Commented by som(math1967) last updated on 17/Oct/20

Are you ex - student of

Baranagar R . K . Mission

Commented by Dwaipayan Shikari last updated on 17/Oct/20

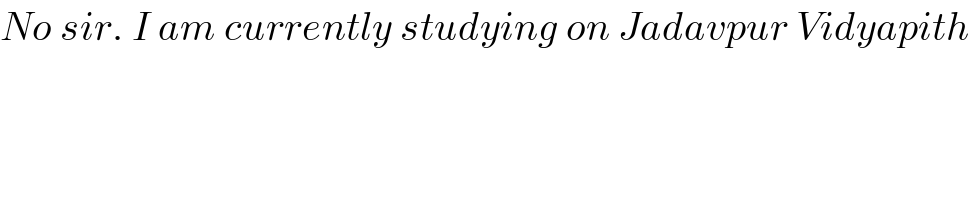
N o s i r . I a m c u r r e n t l y s t u d y i n g o n J a d a v p u r V i d y a p i t h

Commented by som(math1967) last updated on 17/Oct/20

Ok

Commented by Dwaipayan Shikari last updated on 17/Oct/20

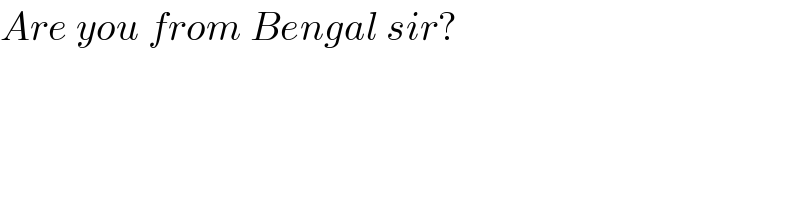
A r e y o u f r o m B e n g a l s i r ?

Commented by som(math1967) last updated on 17/Oct/20

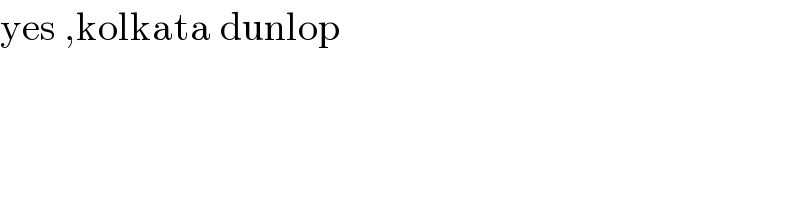
yes, kolkata dunlop

Answered by som(math1967) last updated on 17/Oct/20

\int \frac{\sec^{2} \frac{x}{2} dx}{{3 \sec}^{2} \frac{x}{2} - 5 \times 2 \sin \frac{x}{2} \cos \frac{x}{2} \sec^{2} \frac{x}{2}}

\int \frac{\sec^{2} \frac{x}{2} dx}{3 + {3 \tan}^{2} \frac{x}{2} - 10 \tan \frac{x}{2}}

let \tan \frac{x}{2} = z

\sec^{2} \frac{x}{2} \times \frac{1}{2} dx = dz

\sec^{2} \frac{x}{2} dx = 2 dz

2 \int \frac{dz}{{3 z}^{2} - 10 z + 3}

\frac{2}{3} \int \frac{dz}{z^{2} - \frac{10 z}{3} + 1}

\frac{2}{3} \int \frac{dz}{z^{2} - 2 . z . \frac{5}{3} + \frac{25}{9} + 1 - \frac{25}{9}}

\frac{2}{3} \int \frac{dz}{{(z - \frac{5}{3})}^{2} - {(\frac{4}{3})}^{2}}

\frac{2}{3} \times \frac{3}{2 \times 4} \ln ∣ \frac{z - \frac{5}{3} - \frac{4}{3}}{z - \frac{5}{3} + \frac{4}{3}} ∣ + c

\frac{1}{4} \ln ∣ \frac{z - \frac{9}{3}}{z - \frac{1}{3}} ∣ + c ans

z = \tan \frac{x}{2}

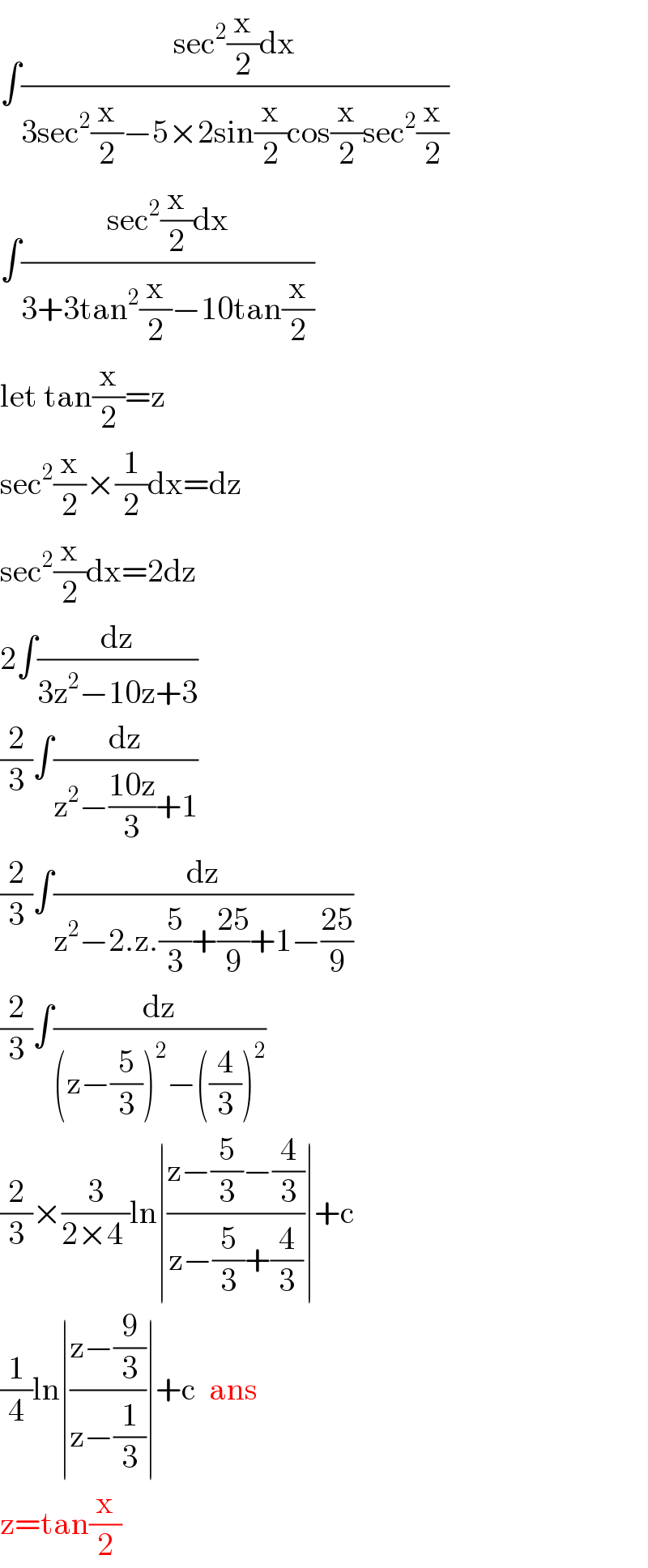
Answered by 1549442205PVT last updated on 17/Oct/20

Put t = \tan \frac{x}{2} \Rightarrow dt = \frac{1}{2} (1 + t^{2}) dx

F = \int \frac{dt}{(t^{2} + 1) (3 - \frac{10 t}{1 + t^{2}})} = \int \frac{2 dt}{({3 t}^{2} - 10 t + 3)}

= \frac{2}{{3 t}^{2} - 10 t + 3} = \frac{a}{3 t - 1} + \frac{b}{t - 3}

\Leftrightarrow 2 = (a + 3 b) t - 3 a - b \Leftrightarrow {\begin{cases} 3 a + b = - 2 \\ a + 3 b = 0 \end{cases}

\Leftrightarrow b = 1 / 4, a = - 3 / 4

F = \frac{- 3}{4} \int \frac{dt}{3 t - 1} + \frac{1}{4} \int \frac{dt}{t - 3} = \frac{1}{4} \ln ∣ \frac{t - 3}{3 t - 1} ∣ + C

= \frac{1}{4} \boldsymbol \ln ∣ \frac{\boldsymbol \tan \frac{\boldsymbol x}{2} - 3}{3 \boldsymbol \tan \frac{\boldsymbol x}{2} - 1} ∣ + \boldsymbol C