Menu Close

solve-dx-x-2-2x-3-x-2-x-3-

Tinku Tara 0 Comments
Pin




Question Number 111615 by mathdave last updated on 04/Sep/20
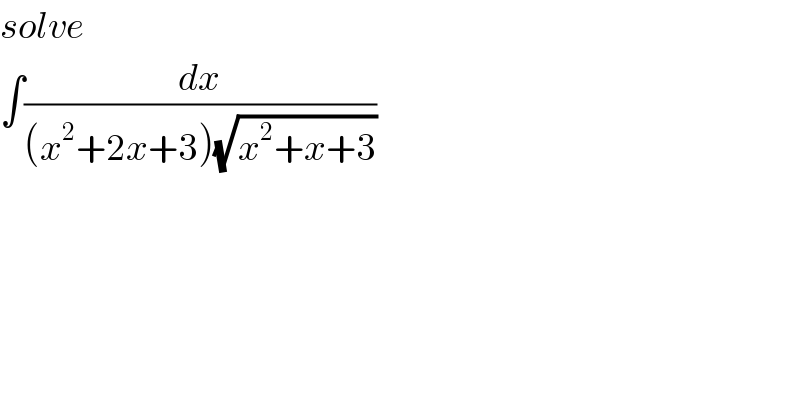
solve ∫(dx/((x^2 +2x+3)(√(x^2 +x+3))))
$${solve} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}} \\ $$
Answered by mathmax by abdo last updated on 04/Sep/20
I =∫ (dx/((x^2 +2x+3)(√(x^2 +x+3)))) ⇒I =∫ (dx/((x^2 +x+3 +x)(√(x^2 +x+3)))) we have x^2 +x +3 =x^2 +((2x)/2) +(1/4) +3−(1/4) =(x+(1/2))^2 +((11)/4) we do the changement x+(1/2) =((√(11))/2) sh(t) ⇒ I =∫ (1/({((11)/4)sh^2 t +((11)/4) +((√(11))/2)sht−(1/2)}((√(11))/2)cht))((√(11))/2) sht dt =4∫ (dt/(11sh^2 t +11 +2(√(11))sht −2)) =4 ∫ (dt/(11sh^2 t +2(√(11))sht +9)) =4∫ (dt/(11((ch(2t)−1)/2)+2 (√(11))sh(t) +9)) 8 ∫ (dt/(11ch(2t)+4(√(11))sht +7)) =8 ∫ (dt/(11((e^(2t) +e^(−2t) )/2)+4(√(11))((e^t −e^(−t) )/2) +7)) =16 ∫ (dt/(11e^(2t) +11e^(−2t) +4(√(11))e^t −4(√(11))e^(−t) +14)) =_(e^t =z) 16 ∫ (dz/(z{ 11z^2 +11z^(−2) +4(√(11))z−4(√(11))z^(−1) +14})) =16 ∫ ((zdz)/(11z^4 +11 +4(√(11))z^3 −4(√(11))z+ 14z^2 )) =16 ∫ ((zdz)/(11z^4 +14z^2 +4(√(11))z^3 +11)) rest decomposition of f(z) =(z/(11z^4 +14z^2 +4(√(11))z^3 +11)) ....be continued....
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{3}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{3}}}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}\:+\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{3}}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}\:+\mathrm{3}\:=\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{2x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:\mathrm{sh}\left(\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{1}}{\left\{\frac{\mathrm{11}}{\mathrm{4}}\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:+\frac{\mathrm{11}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{sht}−\frac{\mathrm{1}}{\mathrm{2}}\right\}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{cht}}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:\mathrm{sht}\:\mathrm{dt} \\ $$$$=\mathrm{4}\int\:\:\frac{\mathrm{dt}}{\mathrm{11sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{11}\:+\mathrm{2}\sqrt{\mathrm{11}}\mathrm{sht}\:−\mathrm{2}}\:=\mathrm{4}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{2}\sqrt{\mathrm{11}}\mathrm{sht}\:+\mathrm{9}} \\ $$$$=\mathrm{4}\int\:\:\frac{\mathrm{dt}}{\mathrm{11}\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{2}\:\sqrt{\mathrm{11}}\mathrm{sh}\left(\mathrm{t}\right)\:+\mathrm{9}} \\ $$$$\mathrm{8}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11ch}\left(\mathrm{2t}\right)+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{sht}\:+\mathrm{7}}\:=\mathrm{8}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11}\frac{\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{11}}\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\:+\mathrm{7}} \\ $$$$=\mathrm{16}\:\int\:\frac{\mathrm{dt}}{\mathrm{11e}^{\mathrm{2t}} \:+\mathrm{11e}^{−\mathrm{2t}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{e}^{\mathrm{t}} −\mathrm{4}\sqrt{\mathrm{11}}\mathrm{e}^{−\mathrm{t}} \:+\mathrm{14}} \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{z}} \:\:\:\mathrm{16}\:\int\:\:\frac{\mathrm{dz}}{\mathrm{z}\left\{\:\mathrm{11z}^{\mathrm{2}} +\mathrm{11z}^{−\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}−\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{−\mathrm{1}} \:+\mathrm{14}\right\}} \\ $$$$=\mathrm{16}\:\:\int\:\:\:\frac{\mathrm{zdz}}{\mathrm{11z}^{\mathrm{4}} \:+\mathrm{11}\:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} −\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}+\:\mathrm{14z}^{\mathrm{2}} } \\ $$$$=\mathrm{16}\:\int\:\frac{\mathrm{zdz}}{\mathrm{11z}^{\mathrm{4}} +\mathrm{14z}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} \:+\mathrm{11}}\:\:\mathrm{rest}\:\mathrm{decomposition}\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}}{\mathrm{11z}^{\mathrm{4}} \:+\mathrm{14z}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} \:+\mathrm{11}}\:….\mathrm{be}\:\mathrm{continued}…. \\ $$
Answered by Her_Majesty last updated on 05/Sep/20
∫(dx/((x^2 +2x+3)(√(x^2 +x+3))))= use t=((√(11))/(11))(2x+1+2(√(x^2 +x+3))) =((16)/(11))∫(t/(t^4 +(4/( (√(11))))t^3 +((14)/(11))t^2 −(4/( (√(11))))t+1))dt t^4 +(4/( (√(11))))t^3 +((14)/(11))t^2 −(4/( (√(11))))t+1= =(t^2 +(2/( (√(11))))(1+(√(2+3(√3))))t+((9+4(√3)+8(√(−1+(√3)))+2(√(2+2(√3))))/(11)))× ×(t^2 +(2/( (√(11))))(1−(√(2+2(√3))))t+((9+4(√3)−8(√(−1+(√3)))−2(√(2+2(√3))))/(11))) and I refuse to decompose it, sorry
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}}= \\ $$$${use}\:{t}=\frac{\sqrt{\mathrm{11}}}{\mathrm{11}}\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{11}}\int\frac{{t}}{{t}^{\mathrm{4}} +\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}^{\mathrm{3}} +\frac{\mathrm{14}}{\mathrm{11}}{t}^{\mathrm{2}} −\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}+\mathrm{1}}{dt} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}^{\mathrm{3}} +\frac{\mathrm{14}}{\mathrm{11}}{t}^{\mathrm{2}} −\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}+\mathrm{1}= \\ $$$$=\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\left(\mathrm{1}+\sqrt{\mathrm{2}+\mathrm{3}\sqrt{\mathrm{3}}}\right){t}+\frac{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{8}\sqrt{−\mathrm{1}+\sqrt{\mathrm{3}}}+\mathrm{2}\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{11}}\right)× \\ $$$$×\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\left(\mathrm{1}−\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}\right){t}+\frac{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{8}\sqrt{−\mathrm{1}+\sqrt{\mathrm{3}}}−\mathrm{2}\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{11}}\right) \\ $$$${and}\:{I}\:{refuse}\:{to}\:{decompose}\:{it},\:{sorry} \\ $$
Commented by mathdave last updated on 05/Sep/20
u c your life why cant u continue the solve has u know book ∙sorry u no nothing
$${u}\:{c}\:{your}\:{life}\:{why}\:{cant}\:{u}\:{continue}\:{the} \\ $$$${solve}\:{has}\:{u}\:{know}\:{book}\:\centerdot{sorry}\:{u}\:{no} \\ $$$${nothing} \\ $$
Commented by mathdave last updated on 05/Sep/20
has u antagonized my working i thought you will give correct evaluation no one is monopoly of knowledge ooo but am nt afraid to say u cant withstand me in mathematics
$${has}\:{u}\:{antagonized}\:{my}\:{working}\:{i} \\ $$$${thought}\:{you}\:{will}\:{give}\:{correct}\:{evaluation} \\ $$$${no}\:{one}\:{is}\:{monopoly}\:{of}\:{knowledge}\:{ooo} \\ $$$${but}\:{am}\:{nt}\:{afraid}\:{to}\:{say}\:{u}\:{cant} \\ $$$${withstand}\:{me}\:{in}\:{mathematics}\: \\ $$
Commented by Her_Majesty last updated on 05/Sep/20
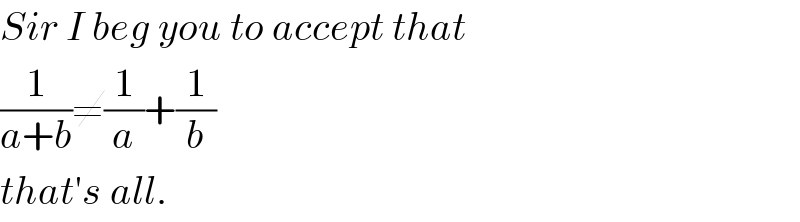
Sir I beg you to accept that (1/(a+b))≠(1/a)+(1/b) that′s all.
$${Sir}\:{I}\:{beg}\:{you}\:{to}\:{accept}\:{that} \\ $$$$\frac{\mathrm{1}}{{a}+{b}}\neq\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}} \\ $$$${that}'{s}\:{all}. \\ $$
Commented by Her_Majesty last updated on 05/Sep/20
btw I can continue but I don′t want to. obviously I′d have to decompose the fraction and solve 2 integrals of the form ∫((at+b)/(t^2 +αt+β))dt but I don′t waste my time with these given constants; I won′t gain any new experience doing so.
$${btw}\:{I}\:{can}\:{continue}\:{but}\:{I}\:{don}'{t}\:{want}\:{to}. \\ $$$${obviously}\:{I}'{d}\:{have}\:{to}\:{decompose}\:{the}\:{fraction} \\ $$$${and}\:{solve}\:\mathrm{2}\:{integrals}\:{of}\:{the}\:{form} \\ $$$$\int\frac{{at}+{b}}{{t}^{\mathrm{2}} +\alpha{t}+\beta}{dt}\:{but}\:{I}\:{don}'{t}\:{waste}\:{my}\:{time}\:{with} \\ $$$${these}\:{given}\:{constants};\:{I}\:{won}'{t}\:{gain}\:{any}\:{new} \\ $$$${experience}\:{doing}\:{so}. \\ $$
Commented by mathdave last updated on 05/Sep/20
tell me what i dont know for this am 101% (very)^(∞ ) and super correct
$${tell}\:{me}\:{what}\:{i}\:{dont}\:{know}\:{for}\:{this}\:{am} \\ $$$$\mathrm{101\%}\:\left({very}\right)^{\infty\:\:} {and}\:{super}\:{correct}\: \\ $$
Commented by mathdave last updated on 05/Sep/20
u most b very very stupid with that big mouth u just said u re mannerless
$${u}\:{most}\:{b}\:{very}\:{very}\:{stupid}\:{with}\:{that}\:{big} \\ $$$${mouth}\:{u}\:{just}\:{said}\:{u}\:{re}\:{mannerless}\: \\ $$
Commented by Her_Majesty last updated on 05/Sep/20
if you solve an integral the test is the derivation. I have shown your result is not correct. ∫f(x)dx=F(x)+C ⇔ (d/dx)[F(x)+C]=f(x) (d/dx)[F(x)+C]≠f(x) ⇒ F(x)+C≠∫f(x)dx prove that I′m wrong or shut up
$${if}\:{you}\:{solve}\:{an}\:{integral}\:{the}\:{test}\:{is}\:{the} \\ $$$${derivation}. \\ $$$${I}\:{have}\:{shown}\:{your}\:{result}\:{is}\:{not}\:{correct}. \\ $$$$\int{f}\left({x}\right){dx}={F}\left({x}\right)+{C}\:\Leftrightarrow\:\frac{{d}}{{dx}}\left[{F}\left({x}\right)+{C}\right]={f}\left({x}\right) \\ $$$$\frac{{d}}{{dx}}\left[{F}\left({x}\right)+{C}\right]\neq{f}\left({x}\right)\:\Rightarrow\:{F}\left({x}\right)+{C}\neq\int{f}\left({x}\right){dx} \\ $$$${prove}\:{that}\:{I}'{m}\:{wrong}\:{or}\:{shut}\:{up} \\ $$
Commented by mathdave last updated on 05/Sep/20
then proceed to do the correct things let me applaud you for the good work .if u cant keep the fuck up let me see views
$${then}\:{proceed}\:{to}\:{do}\:{the}\:{correct}\:{things}\:{let} \\ $$$${me}\:{applaud}\:{you}\:{for}\:{the}\:{good}\:{work}\:.{if}\:{u} \\ $$$${cant}\:{keep}\:{the}\:{fuck}\:{up}\:{let}\:{me}\:{see}\:{views} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *