solve-dy-dx-2-2-y-1-x-y-2-

Question Number 87504 by M±th+et£s last updated on 04/Apr/20

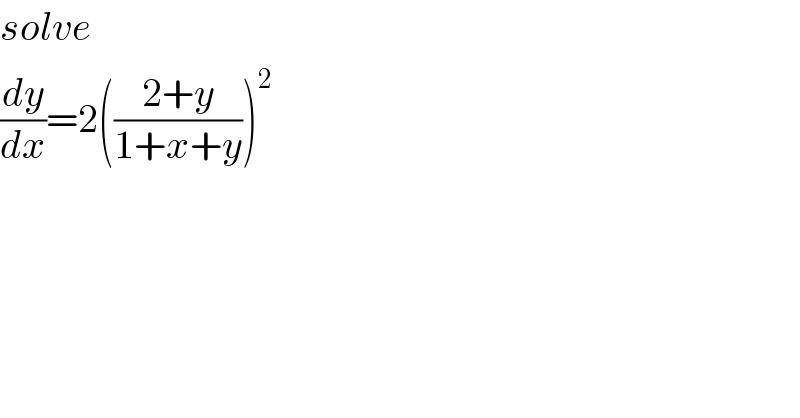
$${solve}\: \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}\left(\frac{\mathrm{2}+{y}}{\mathrm{1}+{x}+{y}}\right)^{\mathrm{2}} \\ $$

Answered by TANMAY PANACEA. last updated on 04/Apr/20

i think (dy/dx)=2(((x+y)/(1+x+y)))^2 t=x+y→(dt/dx)=1+(dy/dx) (dt/dx)−1=2((t/(1+t)))^2 (dt/dx)=1+((2t^2 )/(1+2t+t^2 )) ((1+2t+t^2 )/(3t^2 +2t+1))dt=dx (1/3)∫((3t^2 +2t+1+4t+2)/(3t^2 +2t+1))dt=∫dx ∫dt+(2/3)∫((6t+2+1)/(3t^2 +2t+1))dt=3∫dx ∫dt+(2/3)∫((d(3t^2 +2t+1))/(3t^2 +2t+1))+(2/9)∫(dt/(t^2 +2×t×(1/3)+(1/9)+(1/3)−(1/9)))=3∫dx ∫dt+(2/3)∫((d(3t^2 +2t+1))/(3t^2 +2t+1))+(2/9)∫(dt/((t+(1/3))^2 +(((√2)/3))^2 ))=3∫dx t+(2/3)ln(3t^2 +2t+1)+(2/9)×(3/( (√2)))tan^(−1) (((t+(1/3))/((√2)/3)))=3x+c now pls put t=x+y

$${i}\:{think} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}\left(\frac{{x}+{y}}{\mathrm{1}+{x}+{y}}\right)^{\mathrm{2}} \\ $$$${t}={x}+{y}\rightarrow\frac{{dt}}{{dx}}=\mathrm{1}+\frac{{dy}}{{dx}} \\ $$$$\frac{{dt}}{{dx}}−\mathrm{1}=\mathrm{2}\left(\frac{{t}}{\mathrm{1}+{t}}\right)^{\mathrm{2}} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}{t}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+\mathrm{2}{t}+{t}^{\mathrm{2}} }{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}{dt}={dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}+\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}{dt}=\int{dx} \\ $$$$\int{dt}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{6}{t}+\mathrm{2}+\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}{dt}=\mathrm{3}\int{dx} \\ $$$$\int{dt}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}×{t}×\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}}=\mathrm{3}\int{dx} \\ $$$$\int{dt}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{3}\int{dx} \\ $$$${t}+\frac{\mathrm{2}}{\mathrm{3}}{ln}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)+\frac{\mathrm{2}}{\mathrm{9}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}}\right)=\mathrm{3}{x}+{c} \\ $$$${now}\:{pls}\:{put}\:{t}={x}+{y} \\ $$$$ \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 04/Apr/20