Question Number 51840 by 33 last updated on 31/Dec/18
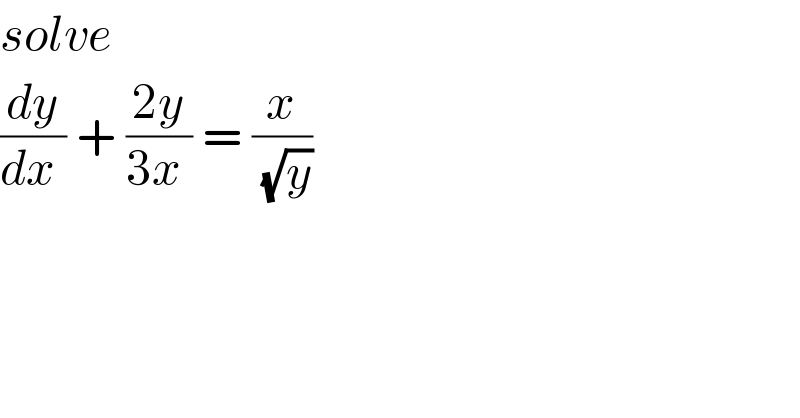
$${solve} \\ $$$$\frac{{dy}}{{dx}\:}\:+\:\frac{\mathrm{2}{y}}{\mathrm{3}{x}\:}\:=\:\frac{{x}}{\:\sqrt{{y}}} \\ $$
Answered by ajfour last updated on 31/Dec/18
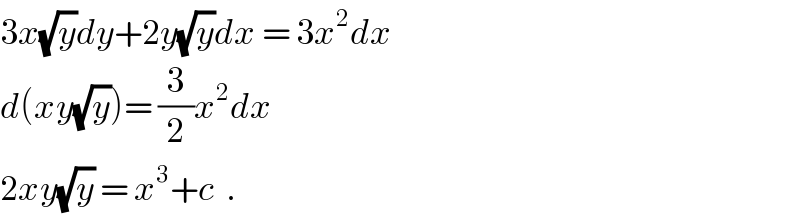
$$\mathrm{3}{x}\sqrt{{y}}{dy}+\mathrm{2}{y}\sqrt{{y}}{dx}\:=\:\mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$${d}\left({xy}\sqrt{{y}}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} {dx} \\ $$$$\mathrm{2}{xy}\sqrt{{y}}\:=\:{x}^{\mathrm{3}} +{c}\:\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 31/Dec/18
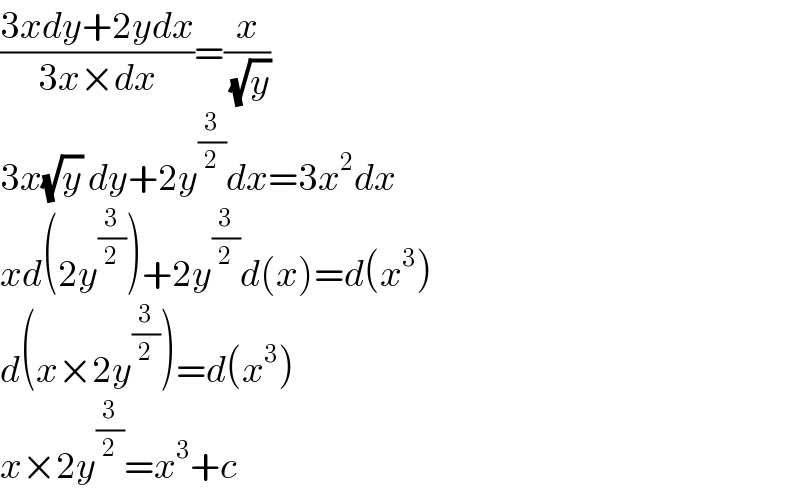
$$\frac{\mathrm{3}{xdy}+\mathrm{2}{ydx}}{\mathrm{3}{x}×{dx}}=\frac{{x}}{\:\sqrt{{y}}} \\ $$$$\mathrm{3}{x}\sqrt{{y}}\:{dy}+\mathrm{2}{y}^{\frac{\mathrm{3}}{\mathrm{2}}} {dx}=\mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$${xd}\left(\mathrm{2}{y}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)+\mathrm{2}{y}^{\frac{\mathrm{3}}{\mathrm{2}}} {d}\left({x}\right)={d}\left({x}^{\mathrm{3}} \right) \\ $$$${d}\left({x}×\mathrm{2}{y}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)={d}\left({x}^{\mathrm{3}} \right) \\ $$$${x}×\mathrm{2}{y}^{\frac{\mathrm{3}}{\mathrm{2}}} ={x}^{\mathrm{3}} +{c} \\ $$
