Question Number 40397 by rahul 19 last updated on 21/Jul/18
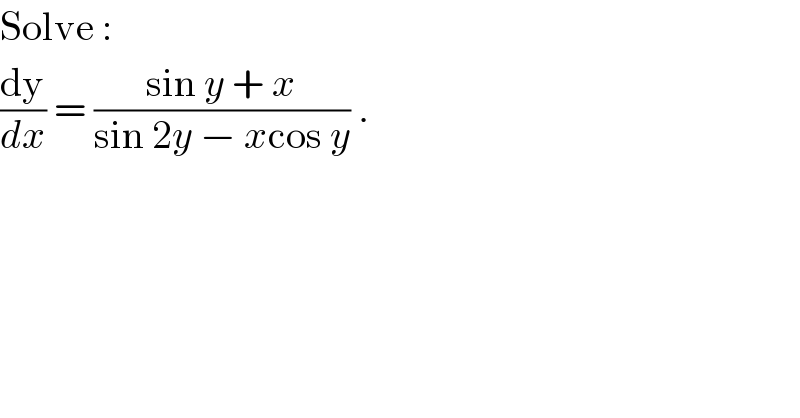
$$\mathrm{Solve}\:: \\ $$$$\frac{\mathrm{dy}}{{dx}}\:=\:\frac{\mathrm{sin}\:{y}\:+\:{x}}{\mathrm{sin}\:\mathrm{2}{y}\:−\:{x}\mathrm{cos}\:{y}}\:. \\ $$
Answered by ajfour last updated on 21/Jul/18
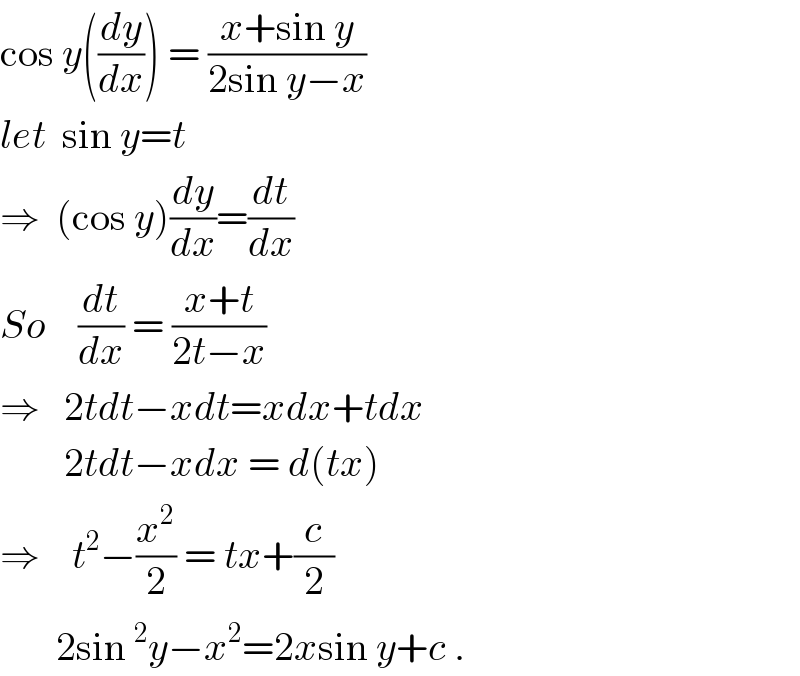
$$\mathrm{cos}\:{y}\left(\frac{{dy}}{{dx}}\right)\:=\:\frac{{x}+\mathrm{sin}\:{y}}{\mathrm{2sin}\:{y}−{x}} \\ $$$${let}\:\:\mathrm{sin}\:{y}={t} \\ $$$$\Rightarrow\:\:\left(\mathrm{cos}\:{y}\right)\frac{{dy}}{{dx}}=\frac{{dt}}{{dx}} \\ $$$${So}\:\:\:\:\frac{{dt}}{{dx}}\:=\:\frac{{x}+{t}}{\mathrm{2}{t}−{x}} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{tdt}−{xdt}={xdx}+{tdx} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{tdt}−{xdx}\:=\:{d}\left({tx}\right) \\ $$$$\Rightarrow\:\:\:\:{t}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:=\:{tx}+\frac{{c}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{2sin}\:^{\mathrm{2}} {y}−{x}^{\mathrm{2}} =\mathrm{2}{x}\mathrm{sin}\:{y}+{c}\:. \\ $$
Commented by rahul 19 last updated on 21/Jul/18
thank you sir ��
