Menu Close

solve-dy-dx-x-y-4-x-y-6-

Tinku Tara 0 Comments
Pin




Question Number 96610 by bemath last updated on 03/Jun/20
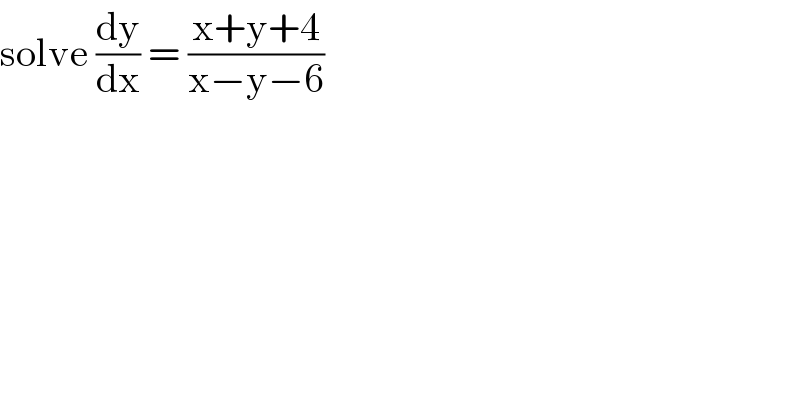
solve (dy/dx) = ((x+y+4)/(x−y−6))
$$\mathrm{solve}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}+\mathrm{y}+\mathrm{4}}{\mathrm{x}−\mathrm{y}−\mathrm{6}} \\ $$
Commented by bobhans last updated on 03/Jun/20
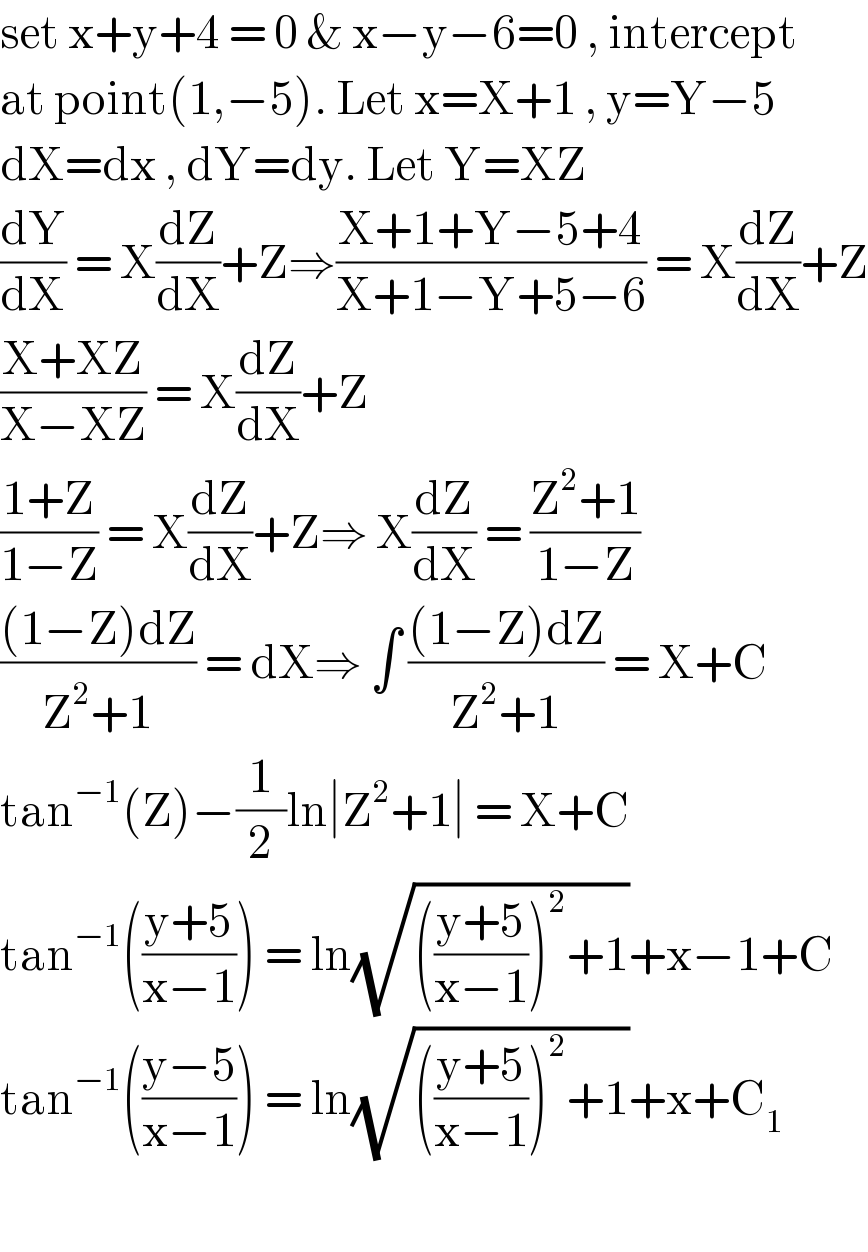
set x+y+4 = 0 & x−y−6=0 , intercept at point(1,−5). Let x=X+1 , y=Y−5 dX=dx , dY=dy. Let Y=XZ (dY/dX) = X(dZ/dX)+Z⇒((X+1+Y−5+4)/(X+1−Y+5−6)) = X(dZ/dX)+Z ((X+XZ)/(X−XZ)) = X(dZ/dX)+Z ((1+Z)/(1−Z)) = X(dZ/dX)+Z⇒ X(dZ/dX) = ((Z^2 +1)/(1−Z)) (((1−Z)dZ)/(Z^2 +1)) = dX⇒ ∫ (((1−Z)dZ)/(Z^2 +1)) = X+C tan^(−1) (Z)−(1/2)ln∣Z^2 +1∣ = X+C tan^(−1) (((y+5)/(x−1))) = ln(√((((y+5)/(x−1)))^2 +1))+x−1+C tan^(−1) (((y−5)/(x−1))) = ln(√((((y+5)/(x−1)))^2 +1))+x+C_1
$$\mathrm{set}\:\mathrm{x}+\mathrm{y}+\mathrm{4}\:=\:\mathrm{0}\:\&\:\mathrm{x}−\mathrm{y}−\mathrm{6}=\mathrm{0}\:,\:\mathrm{intercept} \\ $$$$\mathrm{at}\:\mathrm{point}\left(\mathrm{1},−\mathrm{5}\right).\:\mathrm{Let}\:\mathrm{x}=\mathrm{X}+\mathrm{1}\:,\:\mathrm{y}=\mathrm{Y}−\mathrm{5} \\ $$$$\mathrm{dX}=\mathrm{dx}\:,\:\mathrm{dY}=\mathrm{dy}.\:\mathrm{Let}\:\mathrm{Y}=\mathrm{XZ} \\ $$$$\frac{\mathrm{dY}}{\mathrm{dX}}\:=\:\mathrm{X}\frac{\mathrm{dZ}}{\mathrm{dX}}+\mathrm{Z}\Rightarrow\frac{\mathrm{X}+\mathrm{1}+\mathrm{Y}−\mathrm{5}+\mathrm{4}}{\mathrm{X}+\mathrm{1}−\mathrm{Y}+\mathrm{5}−\mathrm{6}}\:=\:\mathrm{X}\frac{\mathrm{dZ}}{\mathrm{dX}}+\mathrm{Z} \\ $$$$\frac{\mathrm{X}+\mathrm{XZ}}{\mathrm{X}−\mathrm{XZ}}\:=\:\mathrm{X}\frac{\mathrm{dZ}}{\mathrm{dX}}+\mathrm{Z} \\ $$$$\frac{\mathrm{1}+\mathrm{Z}}{\mathrm{1}−\mathrm{Z}}\:=\:\mathrm{X}\frac{\mathrm{dZ}}{\mathrm{dX}}+\mathrm{Z}\Rightarrow\:\mathrm{X}\frac{\mathrm{dZ}}{\mathrm{dX}}\:=\:\frac{\mathrm{Z}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}−\mathrm{Z}} \\ $$$$\frac{\left(\mathrm{1}−\mathrm{Z}\right)\mathrm{dZ}}{\mathrm{Z}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{dX}\Rightarrow\:\int\:\frac{\left(\mathrm{1}−\mathrm{Z}\right)\mathrm{dZ}}{\mathrm{Z}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{X}+\mathrm{C} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{Z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{Z}^{\mathrm{2}} +\mathrm{1}\mid\:=\:\mathrm{X}+\mathrm{C} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{y}+\mathrm{5}}{\mathrm{x}−\mathrm{1}}\right)\:=\:\mathrm{ln}\sqrt{\left(\frac{\mathrm{y}+\mathrm{5}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} +\mathrm{1}}+\mathrm{x}−\mathrm{1}+\mathrm{C} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{y}−\mathrm{5}}{\mathrm{x}−\mathrm{1}}\right)\:=\:\mathrm{ln}\sqrt{\left(\frac{\mathrm{y}+\mathrm{5}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} +\mathrm{1}}+\mathrm{x}+\mathrm{C}_{\mathrm{1}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *