Question Number 40380 by rahul 19 last updated on 21/Jul/18
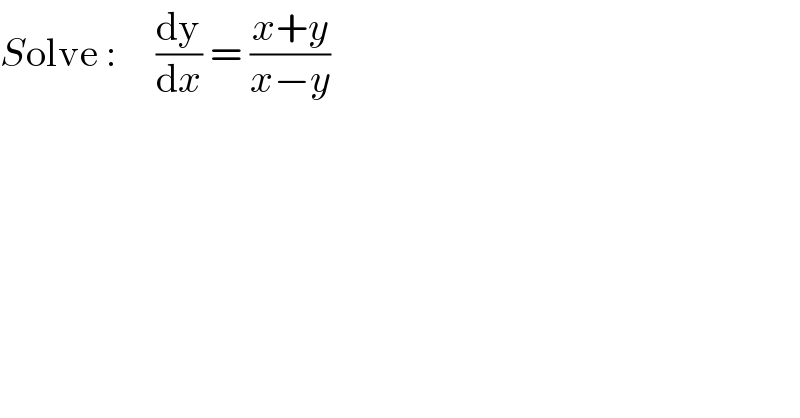
$${S}\mathrm{olve}\::\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{d}{x}}\:=\:\frac{{x}+{y}}{{x}−{y}} \\ $$
Commented by rahul 19 last updated on 21/Jul/18
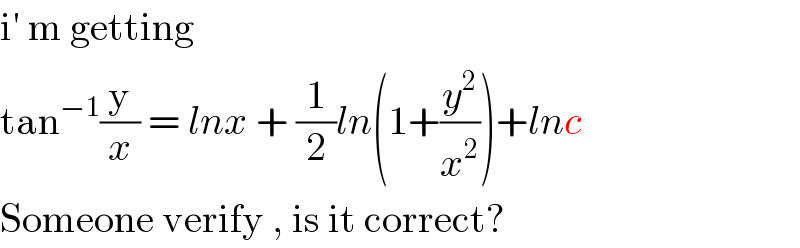
$$\mathrm{i}'\:\mathrm{m}\:\mathrm{getting}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{y}}{{x}}\:=\:{lnx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)+{lnc} \\ $$$$\mathrm{Someone}\:\mathrm{verify}\:,\:\mathrm{is}\:\mathrm{it}\:\mathrm{correct}? \\ $$
Answered by ajfour last updated on 21/Jul/18
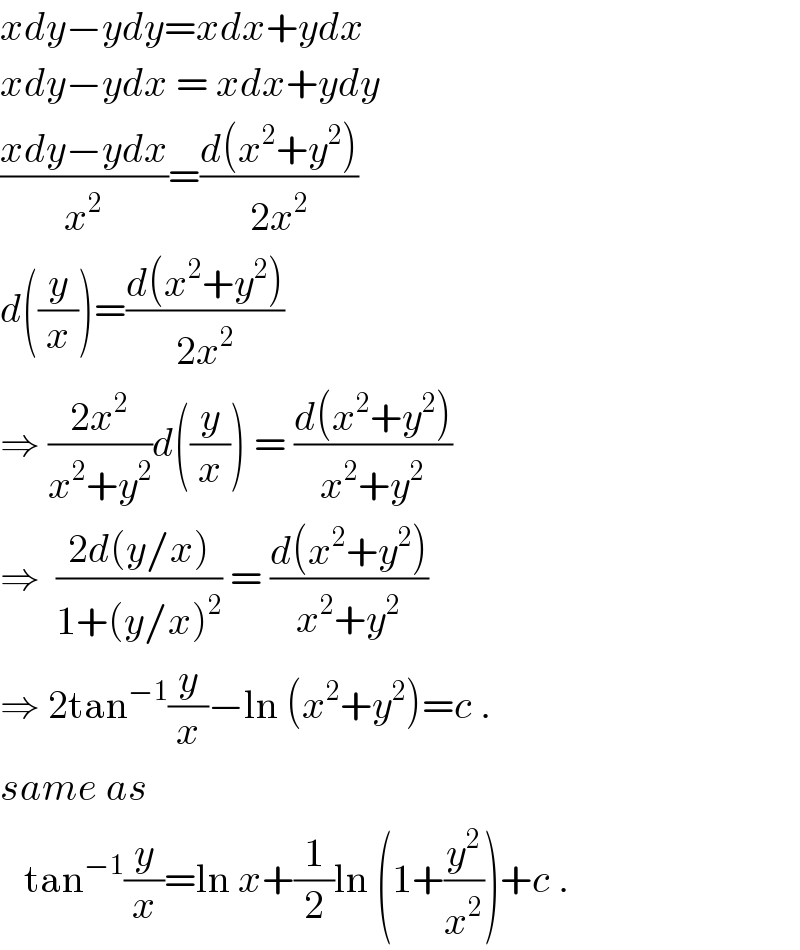
$${xdy}−{ydy}={xdx}+{ydx} \\ $$$${xdy}−{ydx}\:=\:{xdx}+{ydy} \\ $$$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }=\frac{{d}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$${d}\left(\frac{{y}}{{x}}\right)=\frac{{d}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{d}\left(\frac{{y}}{{x}}\right)\:=\:\frac{{d}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{d}\left({y}/{x}\right)}{\mathrm{1}+\left({y}/{x}\right)^{\mathrm{2}} }\:=\:\frac{{d}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{2tan}^{−\mathrm{1}} \frac{{y}}{{x}}−\mathrm{ln}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)={c}\:. \\ $$$${same}\:{as} \\ $$$$\:\:\:\mathrm{tan}^{−\mathrm{1}} \frac{{y}}{{x}}=\mathrm{ln}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)+{c}\:. \\ $$
Commented by rahul 19 last updated on 21/Jul/18
thank you sir ��
Commented by mondodotto@gmail.com last updated on 21/Jul/18
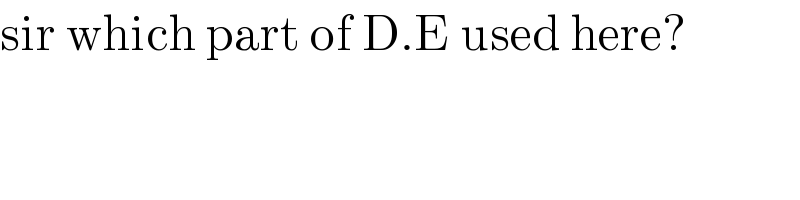
$$\mathrm{sir}\:\mathrm{which}\:\mathrm{part}\:\mathrm{of}\:\mathrm{D}.\mathrm{E}\:\mathrm{used}\:\mathrm{here}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jul/18
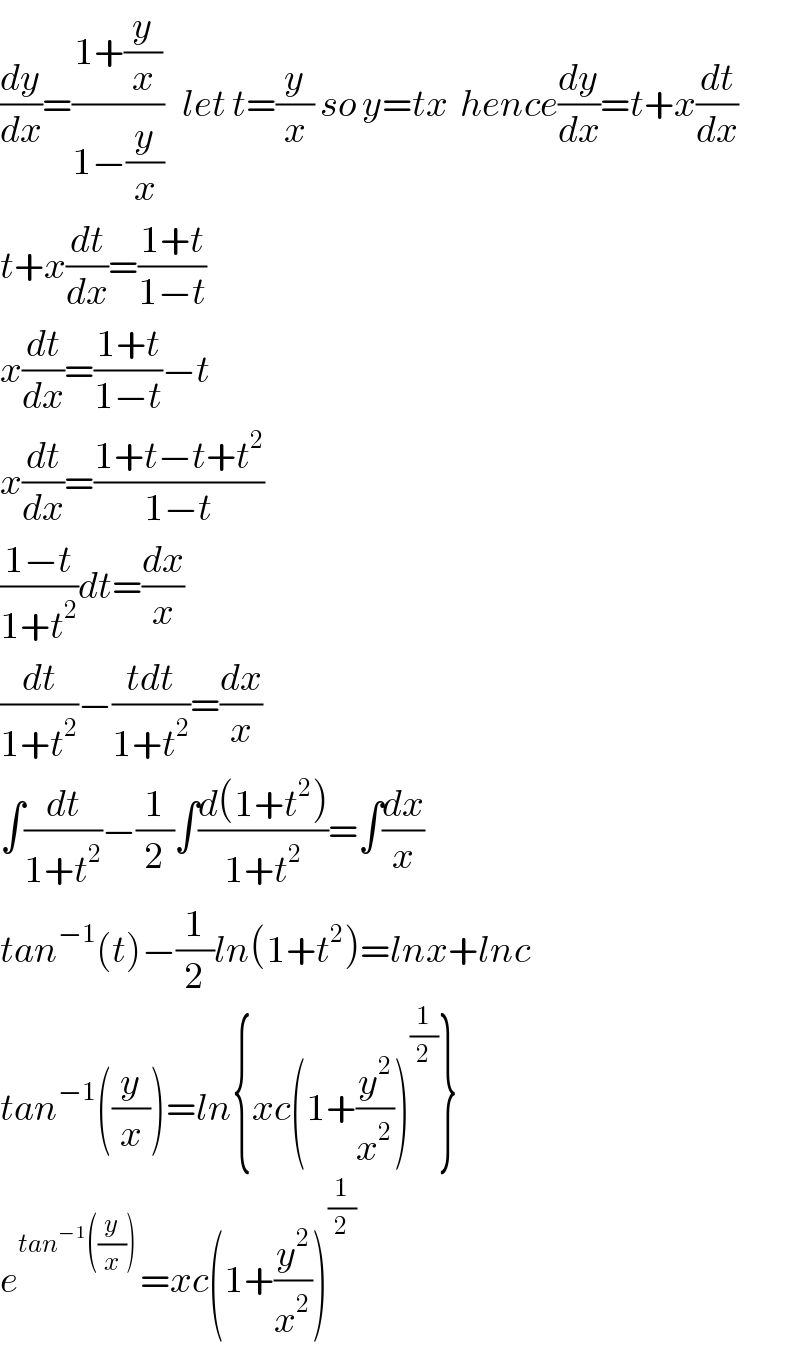
$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}+\frac{{y}}{{x}}}{\mathrm{1}−\frac{{y}}{{x}}}\:\:\:{let}\:{t}=\frac{{y}}{{x}}\:{so}\:{y}={tx}\:\:{hence}\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$${t}+{x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}−{t} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}−{t}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}} \\ $$$$\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{{dx}}{{x}} \\ $$$$\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{{dx}}{{x}} \\ $$$$\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }=\int\frac{{dx}}{{x}} \\ $$$${tan}^{−\mathrm{1}} \left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)={lnx}+{lnc} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)={ln}\left\{{xc}\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right\} \\ $$$${e}^{{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)\:} ={xc}\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Commented by rahul 19 last updated on 21/Jul/18
thank you sir ��
