Question Number 171502 by LEKOUMA last updated on 16/Jun/22
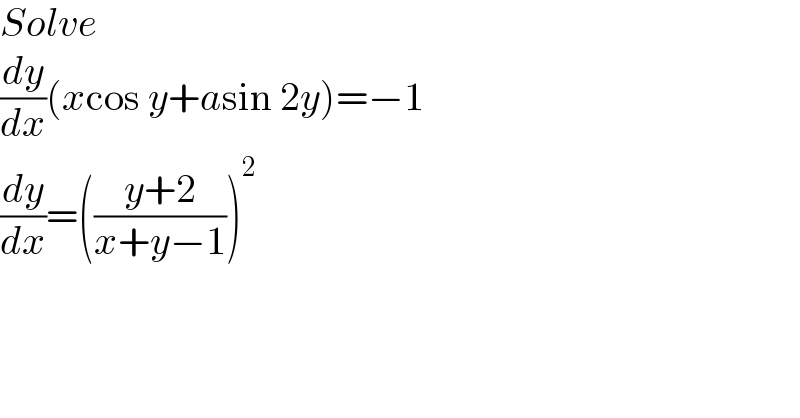
$${Solve} \\ $$$$\frac{{dy}}{{dx}}\left({x}\mathrm{cos}\:{y}+{a}\mathrm{sin}\:\mathrm{2}{y}\right)=−\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=\left(\frac{{y}+\mathrm{2}}{{x}+{y}−\mathrm{1}}\right)^{\mathrm{2}} \\ $$
Commented by mokys last updated on 16/Jun/22
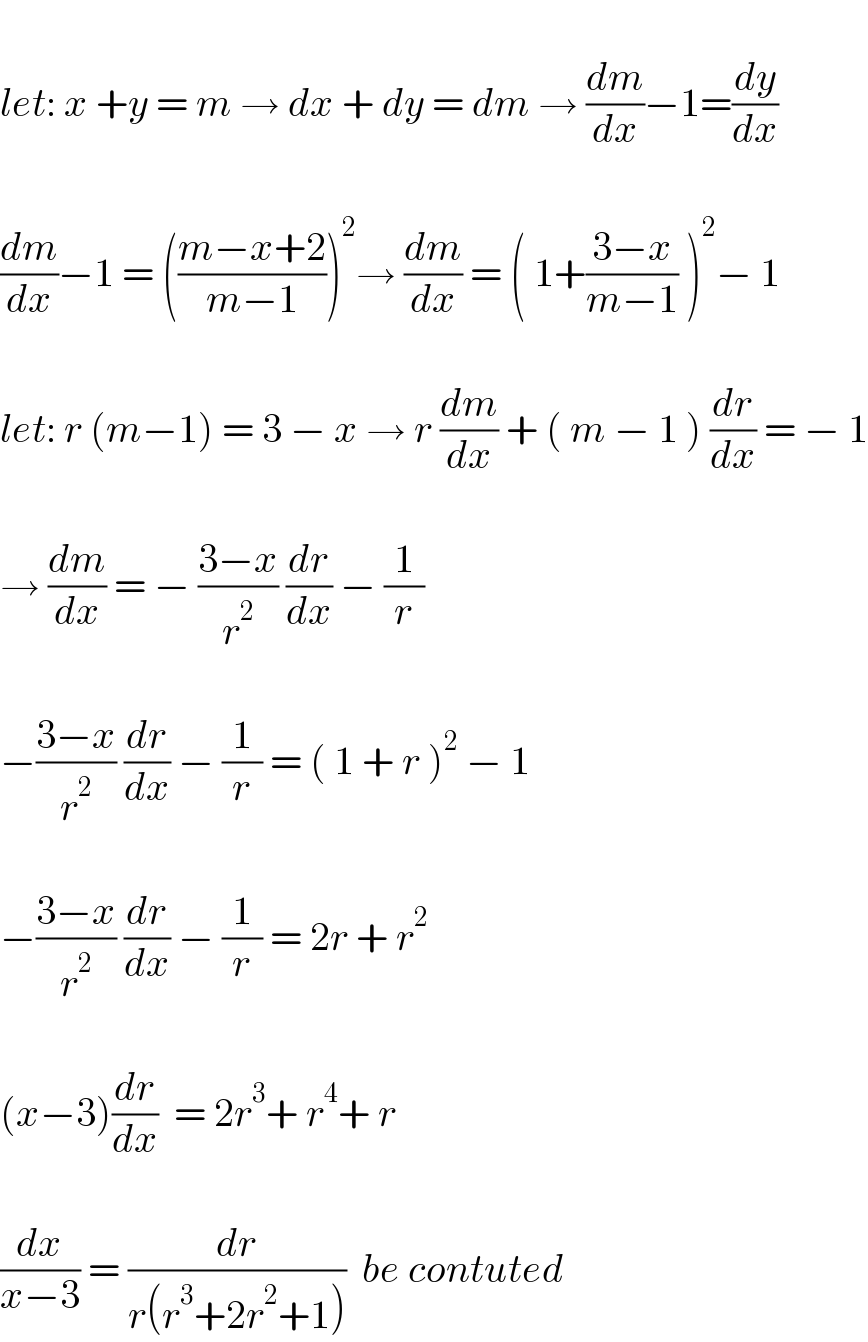
$$ \\ $$$${let}:\:{x}\:+{y}\:=\:{m}\:\rightarrow\:{dx}\:+\:{dy}\:=\:{dm}\:\rightarrow\:\frac{{dm}}{{dx}}−\mathrm{1}=\frac{{dy}}{{dx}} \\ $$$$ \\ $$$$\frac{{dm}}{{dx}}−\mathrm{1}\:=\:\left(\frac{{m}−{x}+\mathrm{2}}{{m}−\mathrm{1}}\right)^{\mathrm{2}} \rightarrow\:\frac{{dm}}{{dx}}\:=\:\left(\:\mathrm{1}+\frac{\mathrm{3}−{x}}{{m}−\mathrm{1}}\:\right)^{\mathrm{2}} −\:\mathrm{1} \\ $$$$ \\ $$$${let}:\:{r}\:\left({m}−\mathrm{1}\right)\:=\:\mathrm{3}\:−\:{x}\:\rightarrow\:{r}\:\frac{{dm}}{{dx}}\:+\:\left(\:{m}\:−\:\mathrm{1}\:\right)\:\frac{{dr}}{{dx}}\:=\:−\:\mathrm{1} \\ $$$$ \\ $$$$\rightarrow\:\frac{{dm}}{{dx}}\:=\:−\:\frac{\mathrm{3}−{x}}{{r}^{\mathrm{2}} }\:\frac{{dr}}{{dx}}\:−\:\frac{\mathrm{1}}{{r}} \\ $$$$ \\ $$$$−\frac{\mathrm{3}−{x}}{{r}^{\mathrm{2}} }\:\frac{{dr}}{{dx}}\:−\:\frac{\mathrm{1}}{{r}}\:=\:\left(\:\mathrm{1}\:+\:{r}\:\right)^{\mathrm{2}} \:−\:\mathrm{1} \\ $$$$ \\ $$$$−\frac{\mathrm{3}−{x}}{{r}^{\mathrm{2}} }\:\frac{{dr}}{{dx}}\:−\:\frac{\mathrm{1}}{{r}}\:=\:\mathrm{2}{r}\:+\:{r}^{\mathrm{2}} \\ $$$$ \\ $$$$\left({x}−\mathrm{3}\right)\frac{{dr}}{{dx}}\:\:=\:\mathrm{2}{r}^{\mathrm{3}} +\:{r}^{\mathrm{4}} +\:{r} \\ $$$$ \\ $$$$\frac{{dx}}{{x}−\mathrm{3}}\:=\:\frac{{dr}}{{r}\left({r}^{\mathrm{3}} +\mathrm{2}{r}^{\mathrm{2}} +\mathrm{1}\right)}\:\:{be}\:{contuted} \\ $$
