Question Number 173572 by mnjuly1970 last updated on 13/Jul/22
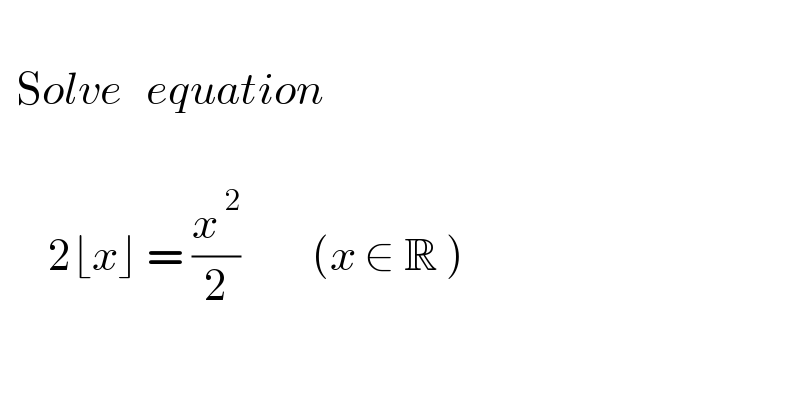
$$\: \\ $$$$\:\:\mathrm{S}{olve}\:\:\:{equation} \\ $$$$ \\ $$$$\:\:\:\:\:\:\mathrm{2}\lfloor{x}\rfloor\:=\:\frac{{x}^{\:\mathrm{2}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\left({x}\:\in\:\mathbb{R}\:\right) \\ $$$$ \\ $$
Answered by MJS_new last updated on 13/Jul/22
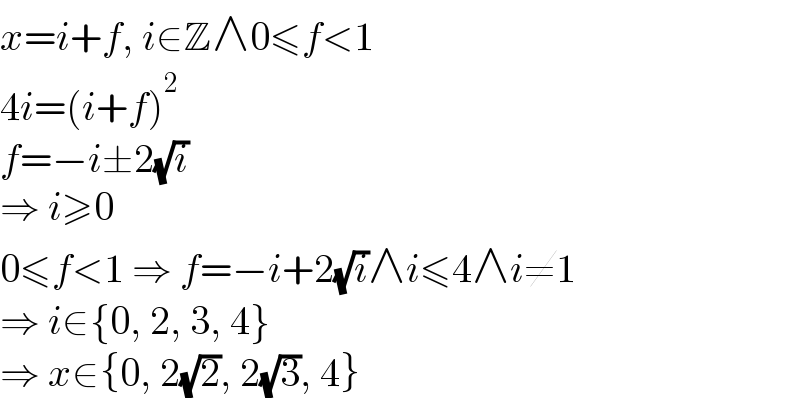
$${x}={i}+{f},\:{i}\in\mathbb{Z}\wedge\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\mathrm{4}{i}=\left({i}+{f}\right)^{\mathrm{2}} \\ $$$${f}=−{i}\pm\mathrm{2}\sqrt{{i}} \\ $$$$\Rightarrow\:{i}\geqslant\mathrm{0} \\ $$$$\mathrm{0}\leqslant{f}<\mathrm{1}\:\Rightarrow\:{f}=−{i}+\mathrm{2}\sqrt{{i}}\wedge{i}\leqslant\mathrm{4}\wedge{i}\neq\mathrm{1} \\ $$$$\Rightarrow\:{i}\in\left\{\mathrm{0},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4}\right\} \\ $$$$\Rightarrow\:{x}\in\left\{\mathrm{0},\:\mathrm{2}\sqrt{\mathrm{2}},\:\mathrm{2}\sqrt{\mathrm{3}},\:\mathrm{4}\right\} \\ $$
Commented by mnjuly1970 last updated on 14/Jul/22
$${thank}\:{you}\:{so}\:{much}.. \\ $$
Answered by mr W last updated on 13/Jul/22
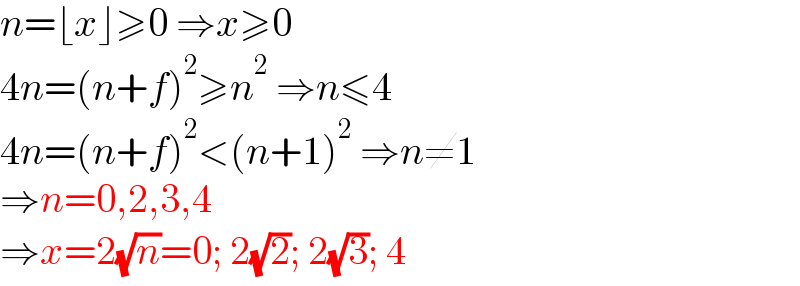
$${n}=\lfloor{x}\rfloor\geqslant\mathrm{0}\:\Rightarrow{x}\geqslant\mathrm{0} \\ $$$$\mathrm{4}{n}=\left({n}+{f}\right)^{\mathrm{2}} \geqslant{n}^{\mathrm{2}} \:\Rightarrow{n}\leqslant\mathrm{4} \\ $$$$\mathrm{4}{n}=\left({n}+{f}\right)^{\mathrm{2}} <\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow{n}\neq\mathrm{1} \\ $$$$\Rightarrow{n}=\mathrm{0},\mathrm{2},\mathrm{3},\mathrm{4} \\ $$$$\Rightarrow{x}=\mathrm{2}\sqrt{{n}}=\mathrm{0};\:\mathrm{2}\sqrt{\mathrm{2}};\:\mathrm{2}\sqrt{\mathrm{3}};\:\mathrm{4} \\ $$
Commented by mnjuly1970 last updated on 14/Jul/22

$$\:{grateful}\:{sir} \\ $$
