solve-f-x-f-f-x-

Question Number 98913 by mr W last updated on 17/Jun/20

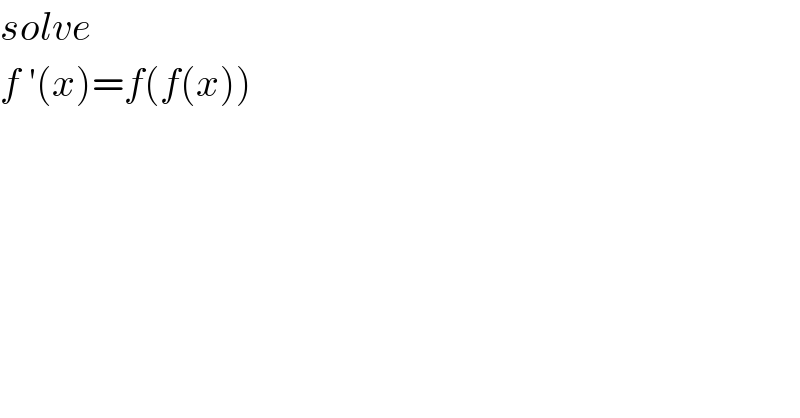
$${solve} \\ $$$${f}\:'\left({x}\right)={f}\left({f}\left({x}\right)\right) \\ $$

Commented by john santu last updated on 17/Jun/20

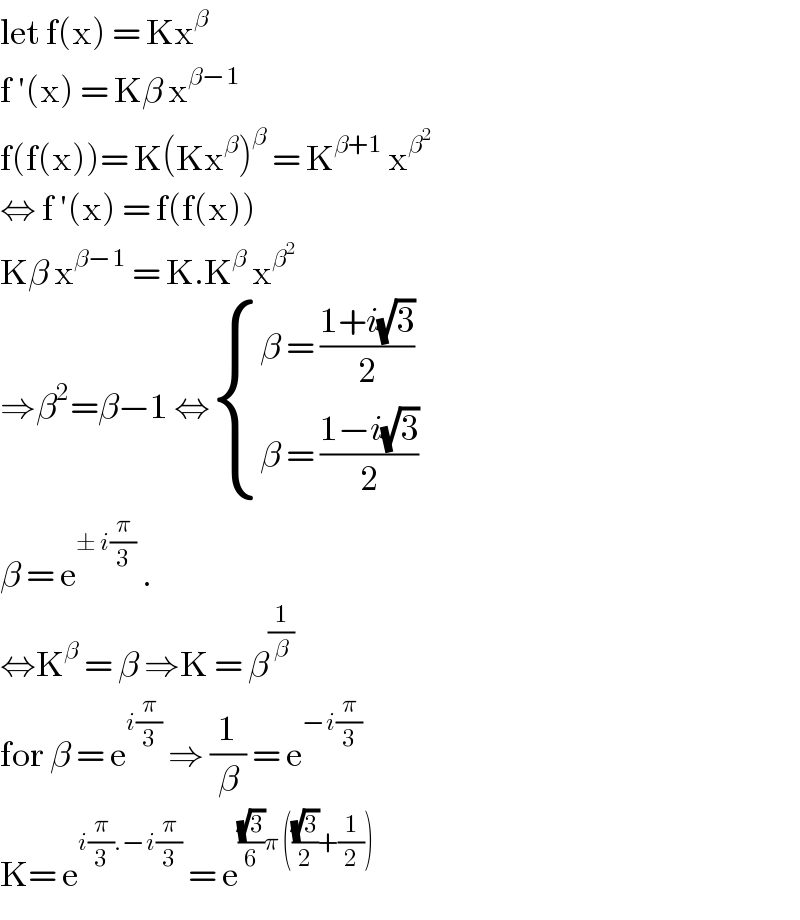
let f(x) = Kx^β f ′(x) = Kβ x^(β−1) f(f(x))= K(Kx^β )^β = K^(β+1) x^β^2 ⇔ f ′(x) = f(f(x)) Kβ x^(β−1) = K.K^β x^β^2 ⇒β^2 =β−1 ⇔ { ((β = ((1+i(√3))/2))),((β = ((1−i(√3))/2))) :} β = e^(± i(π/3)) . ⇔K^β = β ⇒K = β^(1/β) for β = e^(i(π/3)) ⇒ (1/β) = e^(−i(π/3)) K= e^(i(π/3).−i(π/3)) = e^(((√3)/6)π (((√3)/2)+(1/2)))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{Kx}^{\beta} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\mathrm{K}\beta\:\mathrm{x}^{\beta−\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\:\mathrm{K}\left(\mathrm{Kx}^{\beta} \right)^{\beta} \:=\:\mathrm{K}^{\beta+\mathrm{1}} \:\mathrm{x}^{\beta^{\mathrm{2}} } \\ $$$$\Leftrightarrow\:\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\mathrm{K}\beta\:\mathrm{x}^{\beta−\mathrm{1}} \:=\:\mathrm{K}.\mathrm{K}^{\beta} \:\mathrm{x}^{\beta^{\mathrm{2}} } \\ $$$$\Rightarrow\beta^{\mathrm{2}} =\beta−\mathrm{1}\:\Leftrightarrow\begin{cases}{\beta\:=\:\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\beta\:=\:\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{cases} \\ $$$$\beta\:=\:\mathrm{e}^{\pm\:{i}\frac{\pi}{\mathrm{3}}} \:.\: \\ $$$$\Leftrightarrow\mathrm{K}^{\beta} \:=\:\beta\:\Rightarrow\mathrm{K}\:=\:\beta^{\frac{\mathrm{1}}{\beta}} \: \\ $$$$\mathrm{for}\:\beta\:=\:\mathrm{e}^{{i}\frac{\pi}{\mathrm{3}}} \:\Rightarrow\:\frac{\mathrm{1}}{\beta}\:=\:\mathrm{e}^{−{i}\frac{\pi}{\mathrm{3}}} \\ $$$$\mathrm{K}=\:\mathrm{e}^{{i}\frac{\pi}{\mathrm{3}}.−{i}\frac{\pi}{\mathrm{3}}} \:=\:\mathrm{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\pi\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$

Commented by mr W last updated on 17/Jun/20

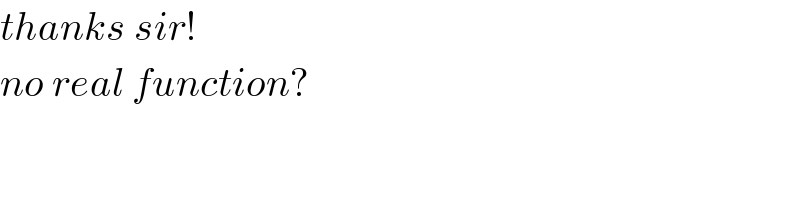
$${thanks}\:{sir}! \\ $$$${no}\:{real}\:{function}? \\ $$

Commented by john santu last updated on 17/Jun/20

$$\mathrm{no}\:\mathrm{sir}.\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply