Question Number 49064 by Rio Michael last updated on 02/Dec/18
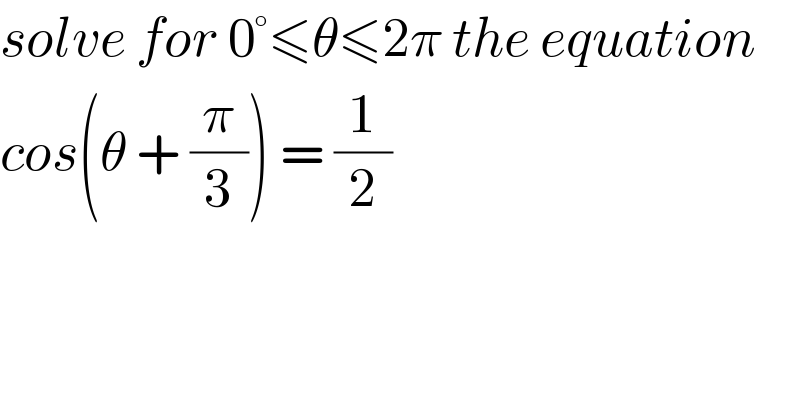
$${solve}\:{for}\:\mathrm{0}°\leqslant\theta\leqslant\mathrm{2}\pi\:{the}\:{equation} \\ $$$${cos}\left(\theta\:+\:\frac{\pi}{\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by hknkrc46 last updated on 02/Dec/18
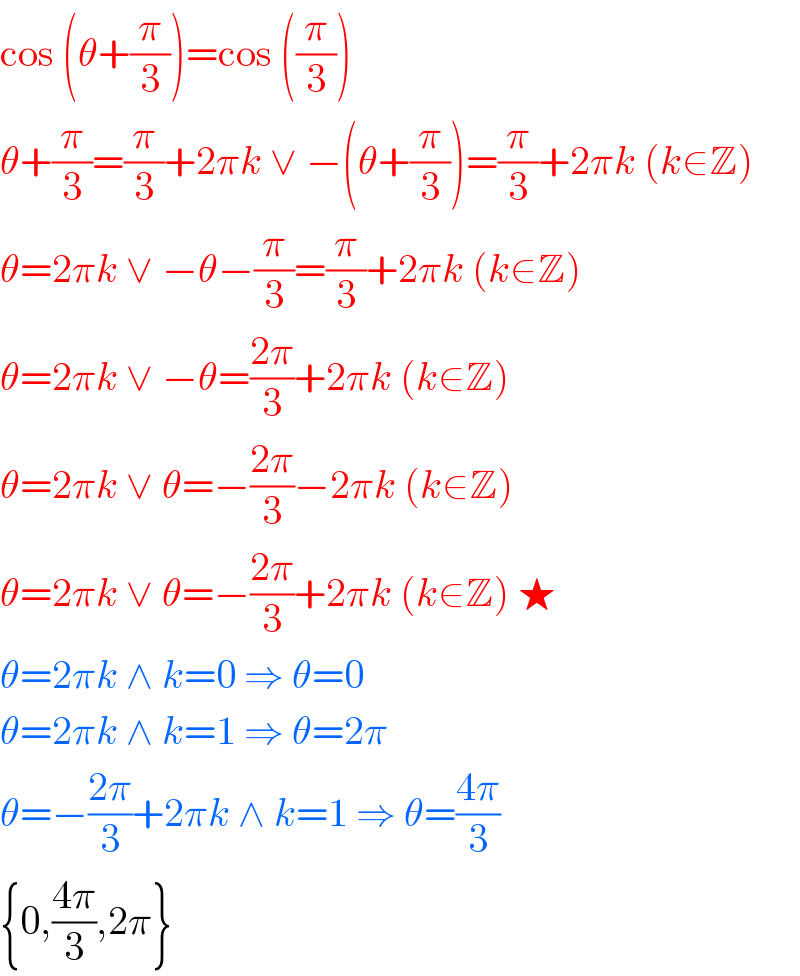
$$\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\theta+\frac{\pi}{\mathrm{3}}=\frac{\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\vee\:−\left(\theta+\frac{\pi}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\left({k}\in\mathbb{Z}\right) \\ $$$$\theta=\mathrm{2}\pi{k}\:\vee\:−\theta−\frac{\pi}{\mathrm{3}}=\frac{\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\left({k}\in\mathbb{Z}\right) \\ $$$$\theta=\mathrm{2}\pi{k}\:\vee\:−\theta=\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\left({k}\in\mathbb{Z}\right) \\ $$$$\theta=\mathrm{2}\pi{k}\:\vee\:\theta=−\frac{\mathrm{2}\pi}{\mathrm{3}}−\mathrm{2}\pi{k}\:\left({k}\in\mathbb{Z}\right) \\ $$$$\theta=\mathrm{2}\pi{k}\:\vee\:\theta=−\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\left({k}\in\mathbb{Z}\right)\:\bigstar \\ $$$$\theta=\mathrm{2}\pi{k}\:\wedge\:{k}=\mathrm{0}\:\Rightarrow\:\theta=\mathrm{0}\: \\ $$$$\theta=\mathrm{2}\pi{k}\:\wedge\:{k}=\mathrm{1}\:\Rightarrow\:\theta=\mathrm{2}\pi \\ $$$$\theta=−\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi{k}\:\wedge\:{k}=\mathrm{1}\:\Rightarrow\:\theta=\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\left\{\mathrm{0},\frac{\mathrm{4}\pi}{\mathrm{3}},\mathrm{2}\pi\right\} \\ $$
