Question Number 36092 by Rio Mike last updated on 28/May/18
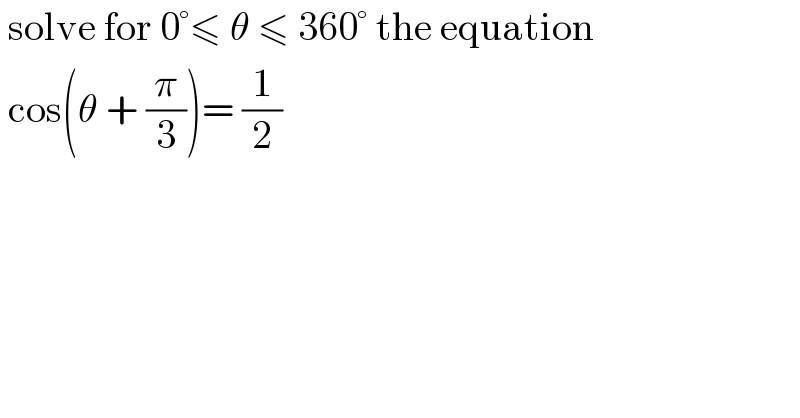
$$\:\mathrm{solve}\:\mathrm{for}\:\mathrm{0}°\leqslant\:\theta\:\leqslant\:\mathrm{360}°\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\mathrm{cos}\left(\theta\:+\:\frac{\pi}{\mathrm{3}}\right)=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by abdo mathsup 649 cc last updated on 30/May/18
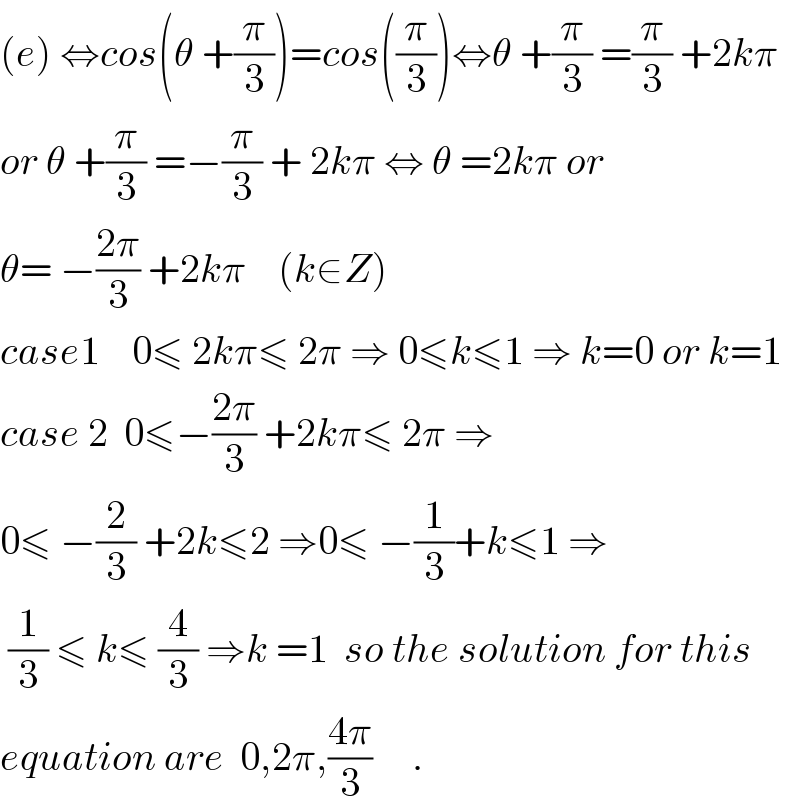
$$\left({e}\right)\:\Leftrightarrow{cos}\left(\theta\:+\frac{\pi}{\mathrm{3}}\right)={cos}\left(\frac{\pi}{\mathrm{3}}\right)\Leftrightarrow\theta\:+\frac{\pi}{\mathrm{3}}\:=\frac{\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi \\ $$$${or}\:\theta\:+\frac{\pi}{\mathrm{3}}\:=−\frac{\pi}{\mathrm{3}}\:+\:\mathrm{2}{k}\pi\:\Leftrightarrow\:\theta\:=\mathrm{2}{k}\pi\:{or}\: \\ $$$$\theta=\:−\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:\:\:\:\left({k}\in{Z}\right) \\ $$$${case}\mathrm{1}\:\:\:\:\mathrm{0}\leqslant\:\mathrm{2}{k}\pi\leqslant\:\mathrm{2}\pi\:\Rightarrow\:\mathrm{0}\leqslant{k}\leqslant\mathrm{1}\:\Rightarrow\:{k}=\mathrm{0}\:{or}\:{k}=\mathrm{1} \\ $$$${case}\:\mathrm{2}\:\:\mathrm{0}\leqslant−\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\leqslant\:\mathrm{2}\pi\:\Rightarrow \\ $$$$\mathrm{0}\leqslant\:−\frac{\mathrm{2}}{\mathrm{3}}\:+\mathrm{2}{k}\leqslant\mathrm{2}\:\Rightarrow\mathrm{0}\leqslant\:−\frac{\mathrm{1}}{\mathrm{3}}+{k}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\:\frac{\mathrm{1}}{\mathrm{3}}\:\leqslant\:{k}\leqslant\:\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow{k}\:=\mathrm{1}\:\:{so}\:{the}\:{solution}\:{for}\:{this} \\ $$$${equation}\:{are}\:\:\mathrm{0},\mathrm{2}\pi,\frac{\mathrm{4}\pi}{\mathrm{3}}\:\:\:\:\:. \\ $$
Answered by Joel579 last updated on 28/May/18
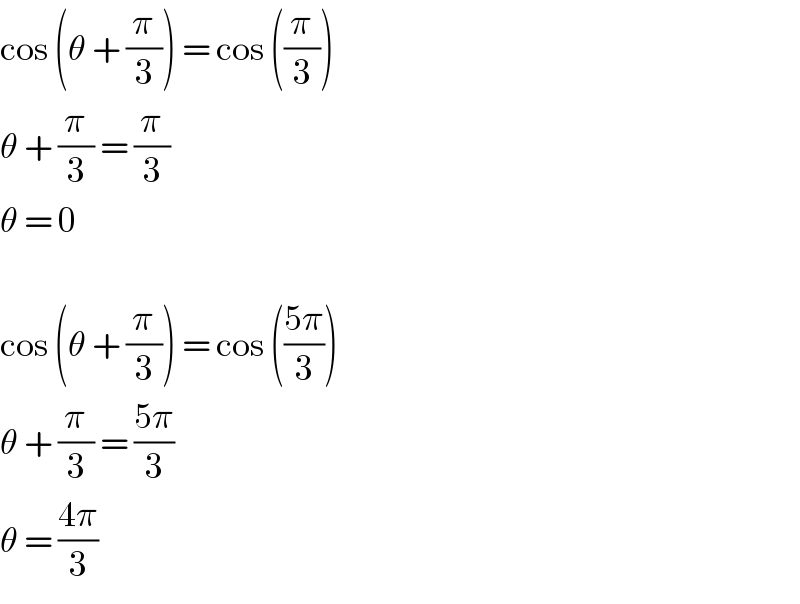
$$\mathrm{cos}\:\left(\theta\:+\:\frac{\pi}{\mathrm{3}}\right)\:=\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\theta\:+\:\frac{\pi}{\mathrm{3}}\:=\:\frac{\pi}{\mathrm{3}} \\ $$$$\theta\:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{cos}\:\left(\theta\:+\:\frac{\pi}{\mathrm{3}}\right)\:=\:\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{3}}\right) \\ $$$$\theta\:+\:\frac{\pi}{\mathrm{3}}\:=\:\frac{\mathrm{5}\pi}{\mathrm{3}} \\ $$$$\theta\:=\:\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$
