Question Number 40285 by MJS last updated on 18/Jul/18

$$\mathrm{solve}\:\mathrm{for}\:\mathrm{1}\:\mathrm{period} \\ $$$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:=\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$\mathrm{sin}\:\frac{\beta}{\mathrm{3}}\:=\mathrm{sin}\:\mathrm{3}\beta \\ $$$$\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}\:=\mathrm{cos}\:\mathrm{2}\gamma \\ $$$$\mathrm{cos}\:\frac{\delta}{\mathrm{3}}\:=\mathrm{cos}\:\mathrm{3}\delta \\ $$$$\mathrm{tan}\:\frac{\epsilon}{\mathrm{2}}\:=\mathrm{tan}\:\mathrm{2}\epsilon \\ $$$$\mathrm{tan}\:\frac{\zeta}{\mathrm{3}}\:=\mathrm{tan}\:\mathrm{3}\zeta \\ $$
Answered by MrW3 last updated on 19/Jul/18

$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:=\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$\Rightarrow\mathrm{2}\alpha+\mathrm{2}{m}\pi=\frac{\alpha}{\mathrm{2}}+\mathrm{2}{n}\pi\Rightarrow\alpha=\frac{\mathrm{4}{k}\pi}{\mathrm{3}} \\ $$$${or} \\ $$$$\Rightarrow\mathrm{2}\alpha+\mathrm{2}{m}\pi=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\frac{\alpha}{\mathrm{2}}\Rightarrow\alpha=\frac{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{5}} \\ $$$$ \\ $$$$\Rightarrow{solution}\:{is}: \\ $$$$\alpha=\frac{\mathrm{4}{k}\pi}{\mathrm{3}}\:{and}\:\alpha=\frac{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{5}}\:{with}\:{k}=\mathrm{0},\pm\mathrm{1},\pm\mathrm{2},… \\ $$$$ \\ $$$${one}\:{period}:\:\mathrm{0}\leqslant\alpha\leqslant\mathrm{4}\pi \\ $$$$\frac{\mathrm{4}{k}\pi}{\mathrm{3}}\leqslant\mathrm{4}\pi\Rightarrow{k}\leqslant\mathrm{3} \\ $$$$\frac{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{5}}\leqslant\mathrm{4}\pi\Rightarrow{k}\leqslant\mathrm{4}.\mathrm{5} \\ $$$$\Rightarrow\alpha=\mathrm{0},\frac{\mathrm{2}\pi}{\mathrm{5}},\frac{\mathrm{6}\pi}{\mathrm{5}},\frac{\mathrm{4}\pi}{\mathrm{3}},\mathrm{2}\pi,\frac{\mathrm{8}\pi}{\mathrm{3}},\frac{\mathrm{14}\pi}{\mathrm{5}},\frac{\mathrm{18}\pi}{\mathrm{5}},\mathrm{4}\pi \\ $$
Answered by MrW3 last updated on 19/Jul/18
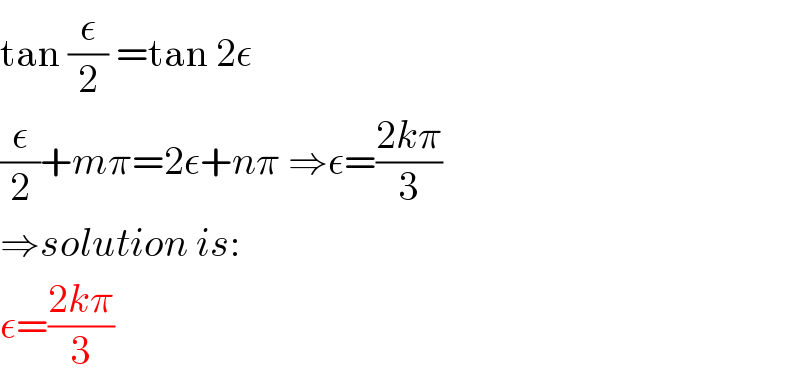
$$\mathrm{tan}\:\frac{\epsilon}{\mathrm{2}}\:=\mathrm{tan}\:\mathrm{2}\epsilon \\ $$$$\frac{\epsilon}{\mathrm{2}}+{m}\pi=\mathrm{2}\epsilon+{n}\pi\:\Rightarrow\epsilon=\frac{\mathrm{2}{k}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{solution}\:{is}: \\ $$$$\epsilon=\frac{\mathrm{2}{k}\pi}{\mathrm{3}} \\ $$
Answered by MrW3 last updated on 19/Jul/18

$$\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}\:=\mathrm{cos}\:\mathrm{2}\gamma \\ $$$$\frac{\gamma}{\mathrm{2}}+\mathrm{2}{m}\pi=\mathrm{2}{n}\pi\pm\mathrm{2}\gamma\Rightarrow\begin{cases}{\gamma=\frac{\mathrm{4}{k}\pi}{\mathrm{3}}}\\{\gamma=\frac{\mathrm{4}{k}\pi}{\mathrm{5}}}\end{cases} \\ $$$$\Rightarrow{solution}\:{is}: \\ $$$$\gamma=\frac{\mathrm{4}{k}\pi}{\mathrm{3}}\:{and}\:\gamma=\frac{\mathrm{4}{k}\pi}{\mathrm{5}} \\ $$
