Question Number 80493 by TawaTawa last updated on 03/Feb/20
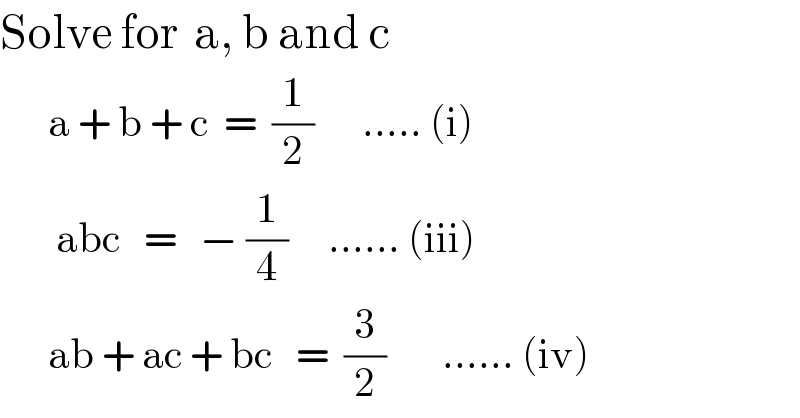
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{a},\:\mathrm{b}\:\mathrm{and}\:\mathrm{c} \\ $$$$\:\:\:\:\:\:\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{abc}\:\:\:=\:\:\:−\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:……\:\left(\mathrm{iii}\right) \\ $$$$\:\:\:\:\:\:\mathrm{ab}\:+\:\mathrm{ac}\:+\:\mathrm{bc}\:\:\:=\:\:\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:……\:\left(\mathrm{iv}\right) \\ $$
Commented by mr W last updated on 03/Feb/20
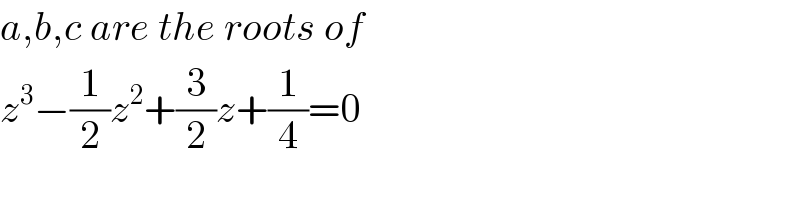
$${a},{b},{c}\:{are}\:{the}\:{roots}\:{of} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{z}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{z}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$
Commented by TawaTawa last updated on 03/Feb/20

$$\mathrm{Sir}\:\mathrm{help}\:\mathrm{me}\:\mathrm{how}\:\mathrm{you}\:\mathrm{derive}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{polynimial} \\ $$
Commented by mr W last updated on 03/Feb/20
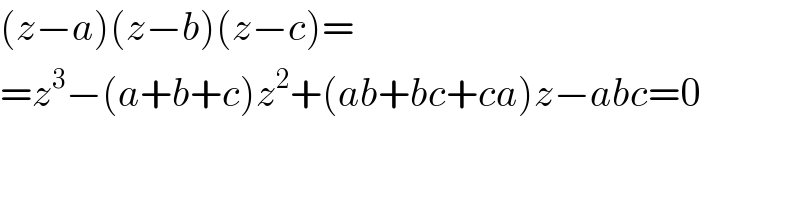
$$\left({z}−{a}\right)\left({z}−{b}\right)\left({z}−{c}\right)= \\ $$$$={z}^{\mathrm{3}} −\left({a}+{b}+{c}\right){z}^{\mathrm{2}} +\left({ab}+{bc}+{ca}\right){z}−{abc}=\mathrm{0} \\ $$
Commented by TawaTawa last updated on 03/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\:\mathrm{appreciate}. \\ $$
