Question Number 148707 by mathdanisur last updated on 30/Jul/21
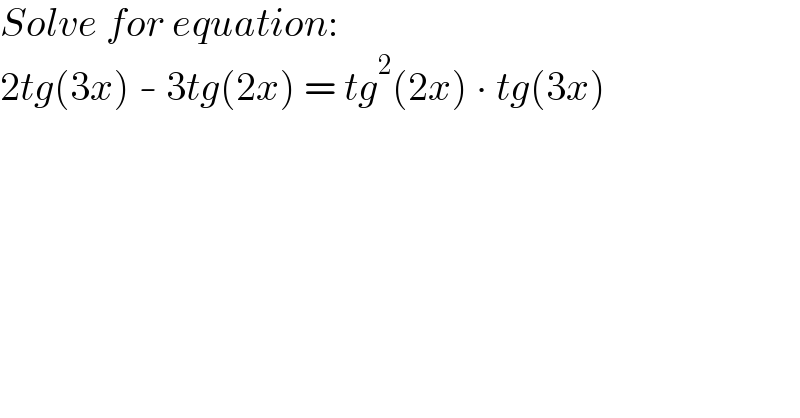
$${Solve}\:{for}\:{equation}: \\ $$$$\mathrm{2}{tg}\left(\mathrm{3}{x}\right)\:-\:\mathrm{3}{tg}\left(\mathrm{2}{x}\right)\:=\:{tg}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:\centerdot\:{tg}\left(\mathrm{3}{x}\right) \\ $$
Answered by nimnim last updated on 30/Jul/21
![Let me give a try.... ⇒2(((3tanx−tan^3 x)/(1−3tan^2 x)))−3(((2tanx)/(1−tan^2 x)))=(((2tanx)/(1−tan^2 x)))^2 (((3tanx−tan^3 x)/(1−3tan^2 x))) ⇒((6tanx−6tan^3 x−2tan^3 x+2tan^5 x−6tanx+18tan^3 x)/((1−3tan^2 x)(1−tan^2 x)))=((4tan^2 x(3tanx−tan^3 x))/((1−tan^2 x)^2 (1−3tan^2 ))) ⇒((2tan^5 x+10tan^3 x)/1)=((4tan^3 x(3−tan^2 x))/(1−tan^2 x)) ⇒2tan^3 x(tan^2 x+5)(1−tan^2 x)−4tan^3 x(3−tan^2 x)=0 ⇒2tan^3 =0 or (tan^2 x+5)(1−tan^2 x)−6+2tan^2 x=0 ⇒tanx=0 or tan^2 x−tan^4 x+5−5tan^2 x−6+2tan^2 x=0 ⇒x=nπ, n∈Z or tan^4 x+2tan^2 x+1=0 or (tan^2 x+1)^2 =0 or tan^2 x+1=0 or sec^2 x=0 or secx=0 but the range of secx is (−∞,−1]∪[1,∞) and zero does not fall within the range. ∴ there is no solution. Hence the only solution is x=nπ, n∈Z](https://www.tinkutara.com/question/Q148722.png)
$${Let}\:{me}\:{give}\:{a}\:{try}…. \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{3}{tanx}−{tan}^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} {x}}\right)−\mathrm{3}\left(\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right)=\left(\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right)^{\mathrm{2}} \left(\frac{\mathrm{3}{tanx}−{tan}^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} {x}}\right) \\ $$$$\Rightarrow\frac{\mathrm{6}{tanx}−\mathrm{6}{tan}^{\mathrm{3}} {x}−\mathrm{2}{tan}^{\mathrm{3}} {x}+\mathrm{2}{tan}^{\mathrm{5}} {x}−\mathrm{6}{tanx}+\mathrm{18}{tan}^{\mathrm{3}} {x}}{\left(\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} {x}\right)\left(\mathrm{1}−{tan}^{\mathrm{2}} {x}\right)}=\frac{\mathrm{4}{tan}^{\mathrm{2}} {x}\left(\mathrm{3}{tanx}−{tan}^{\mathrm{3}} {x}\right)}{\left(\mathrm{1}−{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\frac{\mathrm{2}{tan}^{\mathrm{5}} {x}+\mathrm{10}{tan}^{\mathrm{3}} {x}}{\mathrm{1}}=\frac{\mathrm{4}{tan}^{\mathrm{3}} {x}\left(\mathrm{3}−{tan}^{\mathrm{2}} {x}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$$\Rightarrow\mathrm{2}{tan}^{\mathrm{3}} {x}\left({tan}^{\mathrm{2}} {x}+\mathrm{5}\right)\left(\mathrm{1}−{tan}^{\mathrm{2}} {x}\right)−\mathrm{4}{tan}^{\mathrm{3}} {x}\left(\mathrm{3}−{tan}^{\mathrm{2}} {x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{tan}^{\mathrm{3}} =\mathrm{0}\:{or}\:\left({tan}^{\mathrm{2}} {x}+\mathrm{5}\right)\left(\mathrm{1}−{tan}^{\mathrm{2}} {x}\right)−\mathrm{6}+\mathrm{2}{tan}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\Rightarrow{tanx}=\mathrm{0}\:{or}\:{tan}^{\mathrm{2}} {x}−{tan}^{\mathrm{4}} {x}+\mathrm{5}−\mathrm{5}{tan}^{\mathrm{2}} {x}−\mathrm{6}+\mathrm{2}{tan}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\Rightarrow{x}={n}\pi,\:{n}\in\mathbb{Z}\:\:\:{or}\:\:\:\:{tan}^{\mathrm{4}} {x}+\mathrm{2}{tan}^{\mathrm{2}} {x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:\:\left({tan}^{\mathrm{2}} {x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:\:\:{tan}^{\mathrm{2}} {x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:\:\:{sec}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:\:\:{secx}=\mathrm{0} \\ $$$${but}\:{the}\:{range}\:{of}\:{secx}\:{is}\:\left(−\infty,−\mathrm{1}\right]\cup\left[\mathrm{1},\infty\right)\:{and} \\ $$$${zero}\:{does}\:{not}\:{fall}\:{within}\:{the}\:{range}. \\ $$$$\:\:\:\:\:\:\:\:\:\therefore\:{there}\:{is}\:{no}\:{solution}. \\ $$$${Hence}\:{the}\:{only}\:{solution}\:{is}\:{x}={n}\pi,\:{n}\in\mathbb{Z} \\ $$
Commented by mathdanisur last updated on 30/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
