Question Number 148301 by mathdanisur last updated on 26/Jul/21
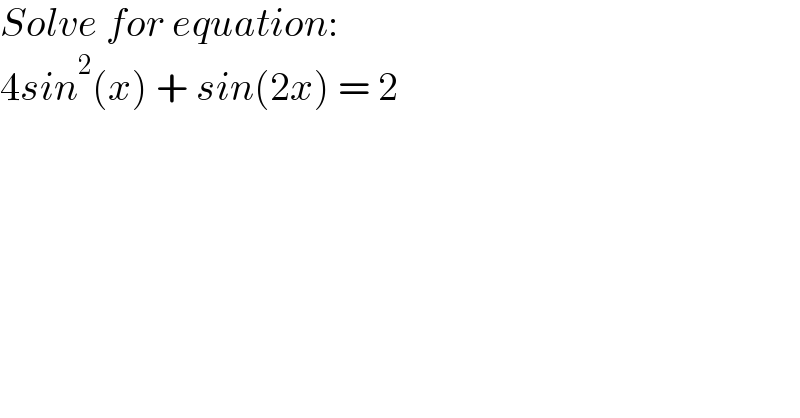
$${Solve}\:{for}\:{equation}: \\ $$$$\mathrm{4}{sin}^{\mathrm{2}} \left({x}\right)\:+\:{sin}\left(\mathrm{2}{x}\right)\:=\:\mathrm{2} \\ $$
Answered by mr W last updated on 27/Jul/21
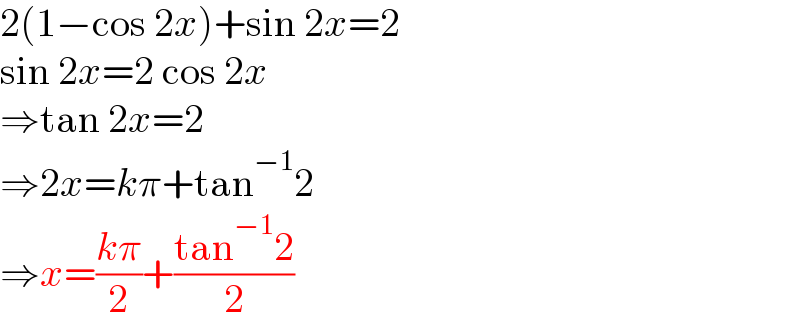
$$\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)+\mathrm{sin}\:\mathrm{2}{x}=\mathrm{2} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}=\mathrm{2}\:\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}{x}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}{x}={k}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{2} \\ $$$$\Rightarrow{x}=\frac{{k}\pi}{\mathrm{2}}+\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{2}}{\mathrm{2}} \\ $$
Commented by puissant last updated on 27/Jul/21

$${wrong} \\ $$
Commented by mathdanisur last updated on 27/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$$${The}\:{answer}\:{is}\:{as}\:{follows}? \\ $$
Commented by mr W last updated on 27/Jul/21
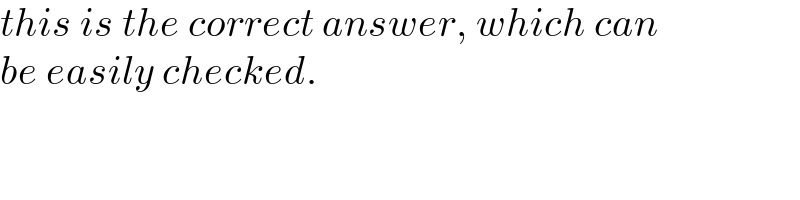
$${this}\:{is}\:{the}\:{correct}\:{answer},\:{which}\:{can} \\ $$$${be}\:{easily}\:{checked}. \\ $$
Commented by mathdanisur last updated on 27/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Commented by mr W last updated on 27/Jul/21
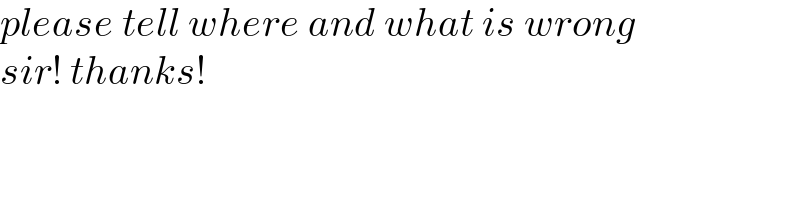
$${please}\:{tell}\:{where}\:{and}\:{what}\:{is}\:{wrong} \\ $$$${sir}!\:{thanks}! \\ $$
