Solve-for-equation-cos-3-x-sin-3-x-1-

Question Number 149025 by mathdanisur last updated on 02/Aug/21

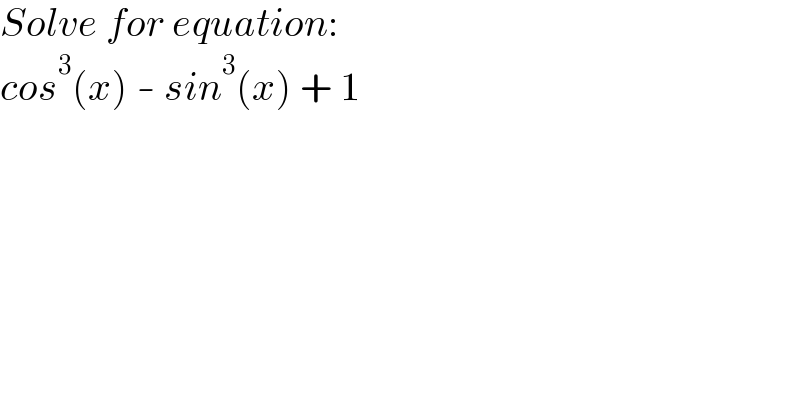
$${Solve}\:{for}\:{equation}: \\ $$$${cos}^{\mathrm{3}} \left({x}\right)\:-\:{sin}^{\mathrm{3}} \left({x}\right)\:+\:\mathrm{1} \\ $$

Commented by ArielVyny last updated on 02/Aug/21

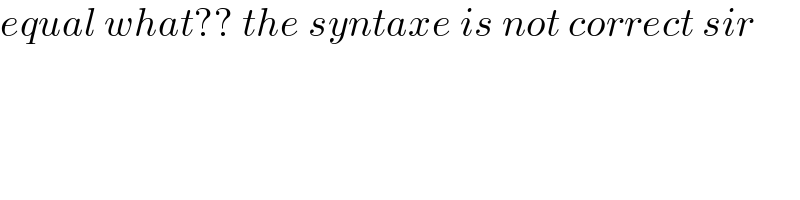
$${equal}\:{what}??\:{the}\:{syntaxe}\:{is}\:{not}\:{correct}\:{sir} \\ $$

Commented by EDWIN88 last updated on 02/Aug/21

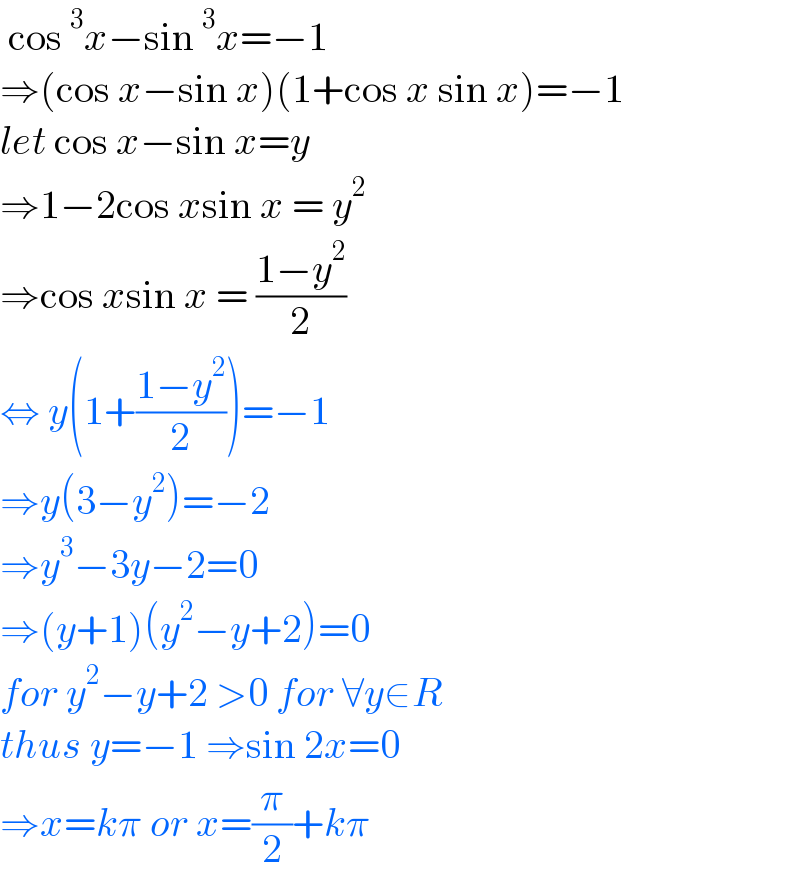
cos^3 x−sin^3 x=−1 ⇒(cos x−sin x)(1+cos x sin x)=−1 let cos x−sin x=y ⇒1−2cos xsin x = y^2 ⇒cos xsin x = ((1−y^2 )/2) ⇔ y(1+((1−y^2 )/2))=−1 ⇒y(3−y^2 )=−2 ⇒y^3 −3y−2=0 ⇒(y+1)(y^2 −y+2)=0 for y^2 −y+2 >0 for ∀y∈R thus y=−1 ⇒sin 2x=0 ⇒x=kπ or x=(π/2)+kπ

$$\:\mathrm{cos}\:^{\mathrm{3}} {x}−\mathrm{sin}\:^{\mathrm{3}} {x}=−\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\right)=−\mathrm{1} \\ $$$${let}\:\mathrm{cos}\:{x}−\mathrm{sin}\:{x}={y}\: \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2cos}\:{x}\mathrm{sin}\:{x}\:=\:{y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\mathrm{sin}\:{x}\:=\:\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Leftrightarrow\:{y}\left(\mathrm{1}+\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{2}}\right)=−\mathrm{1} \\ $$$$\Rightarrow{y}\left(\mathrm{3}−{y}^{\mathrm{2}} \right)=−\mathrm{2} \\ $$$$\Rightarrow{y}^{\mathrm{3}} −\mathrm{3}{y}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\left({y}+\mathrm{1}\right)\left({y}^{\mathrm{2}} −{y}+\mathrm{2}\right)=\mathrm{0} \\ $$$${for}\:{y}^{\mathrm{2}} −{y}+\mathrm{2}\:>\mathrm{0}\:{for}\:\forall{y}\in{R} \\ $$$${thus}\:{y}=−\mathrm{1}\:\Rightarrow\mathrm{sin}\:\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{x}={k}\pi\:{or}\:{x}=\frac{\pi}{\mathrm{2}}+{k}\pi\: \\ $$

Commented by mathdanisur last updated on 02/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$

Answered by MJS_new last updated on 02/Aug/21

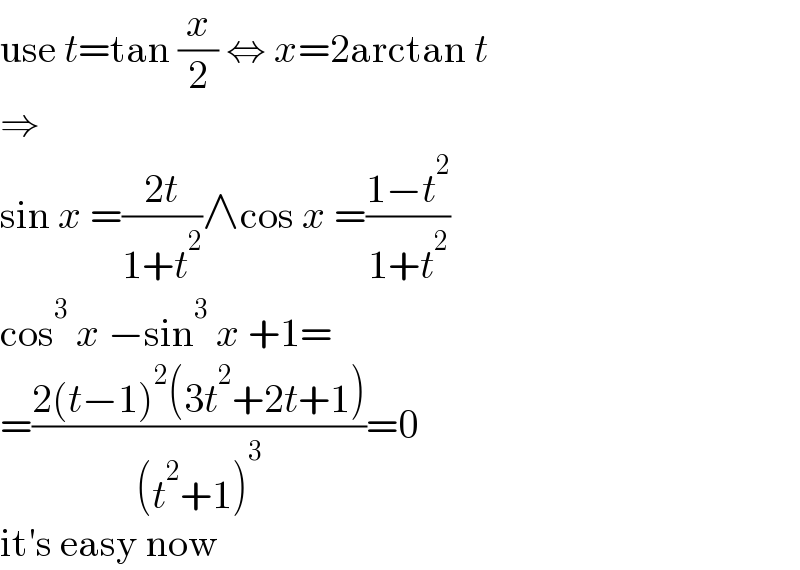
use t=tan (x/2) ⇔ x=2arctan t ⇒ sin x =((2t)/(1+t^2 ))∧cos x =((1−t^2 )/(1+t^2 )) cos^3 x −sin^3 x +1= =((2(t−1)^2 (3t^2 +2t+1))/((t^2 +1)^3 ))=0 it′s easy now

$$\mathrm{use}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\wedge\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{cos}^{\mathrm{3}} \:{x}\:−\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{1}= \\ $$$$=\frac{\mathrm{2}\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{now} \\ $$

Commented by MJS_new last updated on 02/Aug/21

how? well, just solve it what have you learned so far? I doubt you know anything... you want us to solve step by step, we do the job for you. you don′t seem to gain knowledge

$$\mathrm{how}?\:\mathrm{well},\:\mathrm{just}\:\mathrm{solve}\:\mathrm{it} \\ $$$$\mathrm{what}\:\mathrm{have}\:\mathrm{you}\:\mathrm{learned}\:\mathrm{so}\:\mathrm{far}? \\ $$$$\mathrm{I}\:\mathrm{doubt}\:\mathrm{you}\:\mathrm{know}\:\mathrm{anything}… \\ $$$$\mathrm{you}\:\mathrm{want}\:\mathrm{us}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step},\:\mathrm{we}\:\mathrm{do}\:\mathrm{the} \\ $$$$\mathrm{job}\:\mathrm{for}\:\mathrm{you}.\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{gain}\:\mathrm{knowledge} \\ $$

Commented by MJS_new last updated on 02/Aug/21