Question Number 56553 by problem solverd last updated on 18/Mar/19
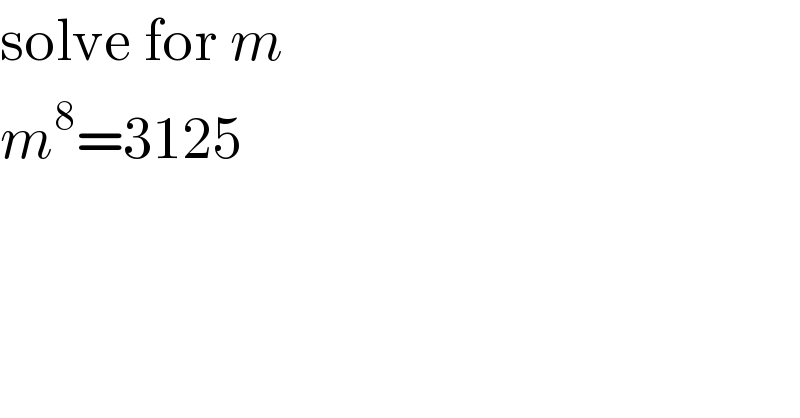
$$\mathrm{solve}\:\mathrm{for}\:{m} \\ $$$${m}^{\mathrm{8}} =\mathrm{3125} \\ $$
Answered by MJS last updated on 18/Mar/19

$${x}^{\mathrm{8}} ={a} \\ $$$$\mathrm{has}\:\mathrm{got}\:\mathrm{8}\:\mathrm{solutions} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\pm\sqrt[{\mathrm{8}}]{{a}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\pm\sqrt[{\mathrm{8}}]{{a}}\mathrm{i} \\ $$$${x}_{\mathrm{5},\:\mathrm{6},\:\mathrm{7},\:\mathrm{8}} =\pm\sqrt[{\mathrm{8}}]{{a}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}\right) \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${m}_{\mathrm{1},\:\mathrm{2}} =\pm\mathrm{5}^{\mathrm{5}/\mathrm{8}} \approx\pm\mathrm{2}.\mathrm{7344} \\ $$$${m}_{\mathrm{3},\:\mathrm{4}} =\pm\mathrm{5}^{\mathrm{5}/\mathrm{8}} \mathrm{i}\approx\pm\mathrm{2}.\mathrm{7344i} \\ $$$${m}_{\mathrm{5},\:\mathrm{6},\:\mathrm{7},\:\mathrm{8}} =\pm\mathrm{5}^{\mathrm{5}/\mathrm{8}} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}\right)\approx\pm\mathrm{1}.\mathrm{9335}\pm\mathrm{1}.\mathrm{9335i} \\ $$
