Solve-for-n-4-n-2-n-6-2-n-4-3-4-n-2-3-

Question Number 47139 by Tawa1 last updated on 05/Nov/18

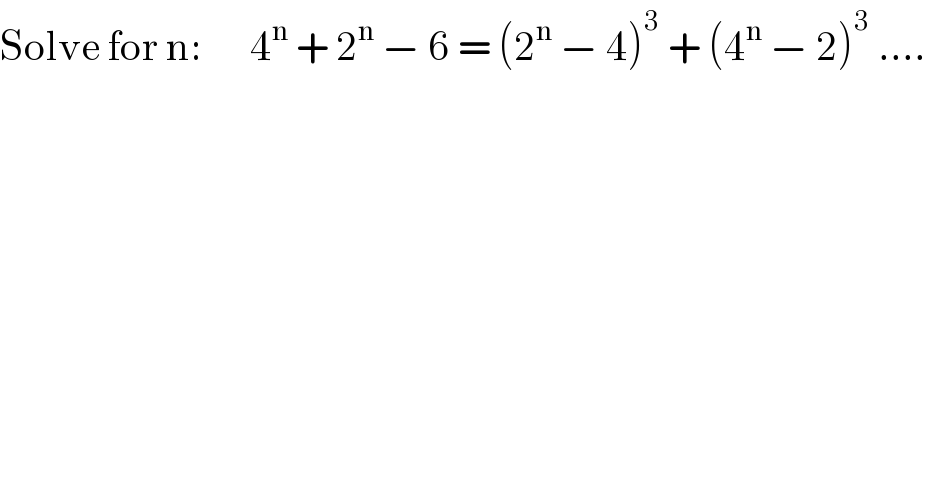
Solve for n : 4^{n} + 2^{n} - 6 = {(2^{n} - 4)}^{3} + {(4^{n} - 2)}^{3} \dots .

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18

2^{n} = x

x^{2} + x - 6 = {(x - 4)}^{3} + {(x^{2} - 2)}^{3}

(x^{2} + x - 6) = (x^{2} + x - 6) {{(x - 4)}^{2} - (x - 4) (x^{2} - 2) + {(x^{2} - 2)}^{2}}

(x^{2} + x - 6) [{x^{2} - 8 x + 16 - x^{3} + 2 x + 4 x^{2} - 8 + x^{4} - 4 x^{2} + 4} - 1] = 0

e i t h e r

x^{2} + x - 6 = 0

x^{2} + 3 x - 2 x - 6 = 0

x (x + 3) - 2 (x + 3) = 0

(x + 3) (x - 2) = 0

x = - 3 x = 2

s o 2^{n} = 2 n = 1 \leftarrow n = 1

2^{n} = - 3

n = {l n}_{2} (- 3) \leftarrow n o t f e a s i b l e s o l u t i o n

a g a i n \dots

[{x^{2} - 8 x + 16 - x^{3} + 2 x + 4 x^{2} - 8 + x^{4} - 4 x^{2} + 4 - 1] = 0

x^{4} - x^{3} + x^{2} - 6 x - 11 = 0

s o l j t i o n a r e 2.4077 a n d - 1.12227

2^{n} = 2.4077

n = {l n}_{2} (2.4077)

2^{n} = - 1.2227

n = {l n}_{2} (- 1.1227) \leftarrow n o g f e a s i b l e s o l u u t i o n

s o n = (1 a n d {l n}_{2} 2.4077)

Commented by Tawa1 last updated on 05/Nov/18

God bless you sir

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18