Question Number 150559 by mathdanisur last updated on 13/Aug/21

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{natural}\:\mathrm{numbers}: \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{4}} \:=\:\mathrm{2022} \\ $$
Answered by MJS_new last updated on 13/Aug/21
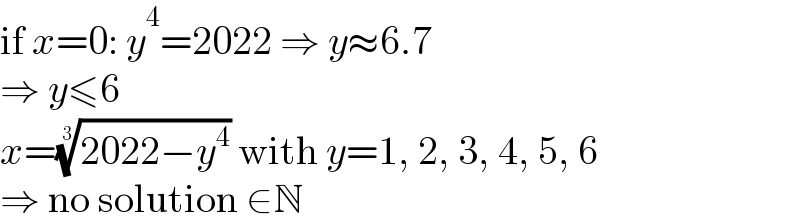
$$\mathrm{if}\:{x}=\mathrm{0}:\:{y}^{\mathrm{4}} =\mathrm{2022}\:\Rightarrow\:{y}\approx\mathrm{6}.\mathrm{7} \\ $$$$\Rightarrow\:{y}\leqslant\mathrm{6} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\mathrm{2022}−{y}^{\mathrm{4}} }\:\mathrm{with}\:{y}=\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\in\mathbb{N} \\ $$
Commented by mathdanisur last updated on 13/Aug/21
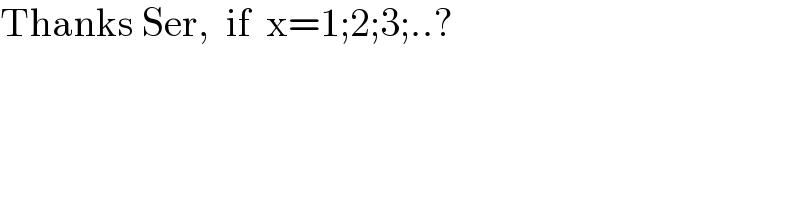
$$\mathrm{Thanks}\:\mathrm{Ser},\:\:\mathrm{if}\:\:\mathrm{x}=\mathrm{1};\mathrm{2};\mathrm{3};..? \\ $$
Commented by MJS_new last updated on 13/Aug/21
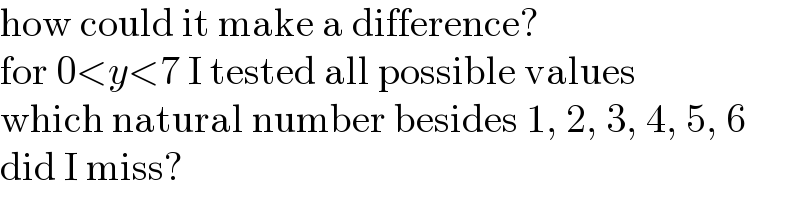
$$\mathrm{how}\:\mathrm{could}\:\mathrm{it}\:\mathrm{make}\:\mathrm{a}\:\mathrm{difference}? \\ $$$$\mathrm{for}\:\mathrm{0}<{y}<\mathrm{7}\:\mathrm{I}\:\mathrm{tested}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{values} \\ $$$$\mathrm{which}\:\mathrm{natural}\:\mathrm{number}\:\mathrm{besides}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6} \\ $$$$\mathrm{did}\:\mathrm{I}\:\mathrm{miss}? \\ $$
Commented by mathdanisur last updated on 14/Aug/21

$$\mathrm{Thankyou}\:\mathrm{Ser} \\ $$
