Question Number 157258 by MathSh last updated on 21/Oct/21
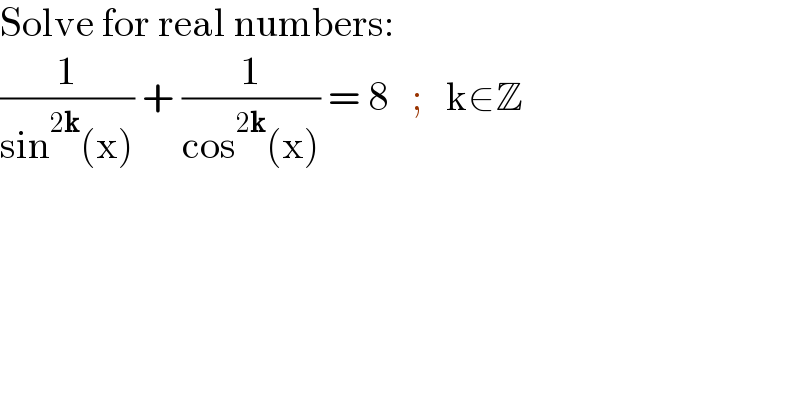
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}\boldsymbol{\mathrm{k}}} \left(\mathrm{x}\right)}\:+\:\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}\boldsymbol{\mathrm{k}}} \left(\mathrm{x}\right)}\:=\:\mathrm{8}\:\:\:;\:\:\:\mathrm{k}\in\mathbb{Z} \\ $$
Commented by mr W last updated on 21/Oct/21

$$\left(\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:{x}}\overset{{k}} {\right)}+\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}\right)^{{k}} \geqslant\mathrm{2}\left(\frac{\mathrm{4}}{\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}\right)^{{k}/\mathrm{2}} \geqslant\mathrm{2}^{{k}+\mathrm{1}} \\ $$$${that}\:{means}\:{for}\:{k}\geqslant\mathrm{3},\:{LHS}\geqslant\mathrm{16}\:\Rightarrow{no}\:{solution}\:{for}\:{LHS}=\mathrm{8}! \\ $$$${for}\:{k}=\mathrm{0}:\:\mathrm{1}+\mathrm{1}=\mathrm{8}\:\Rightarrow{no}\:{solution}! \\ $$$${for}\:{k}\leqslant−\mathrm{1}:\:{LHS}\leqslant\mathrm{2}\:\Rightarrow{no}\:{solution}\:{for}\:{LHS}=\mathrm{8}! \\ $$$${therefore}\:{the}\:{only}\:{possibility}\:{is}\:{k}=\mathrm{1}\:{or}\:\mathrm{2}. \\ $$$$ \\ $$$${k}=\mathrm{1}: \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:{x}}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{8} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{8} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}{x}={n}\pi\pm\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{8}}\:{for}\:{k}=\mathrm{1} \\ $$$$ \\ $$$${k}=\mathrm{2}: \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} \:{x}}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{4}} \:{x}}=\mathrm{8} \\ $$$$\frac{\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{cos}^{\mathrm{4}} \:{x}}{\left(\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\right)^{\mathrm{4}} }=\mathrm{8} \\ $$$$\frac{\left(\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}{\mathrm{2}}\right)\mathrm{16}}{\mathrm{sin}^{\mathrm{4}} \:\mathrm{2}{x}}=\mathrm{8} \\ $$$$\frac{\left(\mathrm{2}−\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}{\mathrm{1}}\right)}{\mathrm{sin}^{\mathrm{4}} \:\mathrm{2}{x}}=\mathrm{1} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}+\mathrm{2}\right)\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}=\pm\mathrm{1} \\ $$$$\mathrm{2}{x}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{4}}\:{for}\:{k}=\mathrm{2} \\ $$
Commented by MathSh last updated on 21/Oct/21
$$\mathrm{Perfect}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
