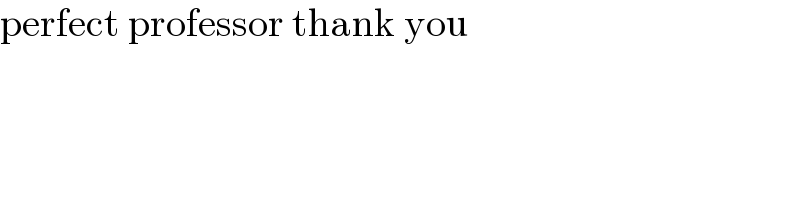Question Number 173184 by Shrinava last updated on 07/Jul/22
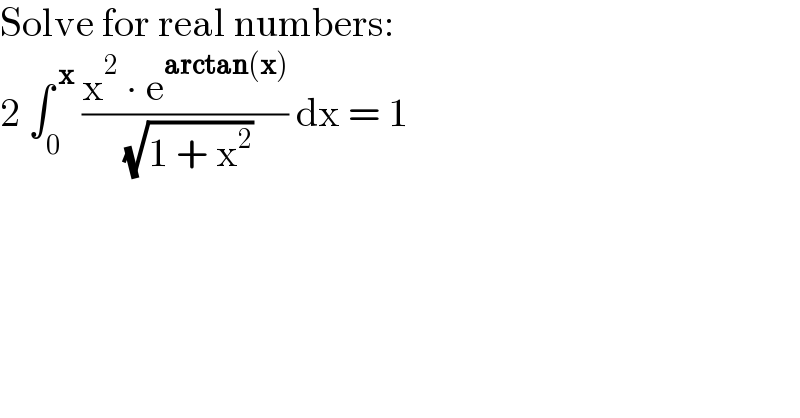
Answered by aleks041103 last updated on 08/Jul/22
![x=tan t dx=sec^2 t dt ⇒2∫_0 ^( t) ((tan^2 tsec^2 t e^t dt)/(sec t))=2∫_0 ^( t) ((sin^2 t)/(cos^3 t))e^t dt= =2∫_0 ^( t) sin t e^t ((sin t)/(cos^3 t))dt= =∫_0 ^( 1) sin t e^t (−2((d(cos t))/((cos t)^3 )))= =∫_0 ^t sint e^t d((1/(cos^2 t)))= =[((sint)/(cos^2 t))e^t ]_0 ^t −∫_0 ^( t) ((cos t e^t + sin t e^t )/(cos^2 t)) dt= =((sint)/(cos^2 t))e^t −∫_0 ^( t) (e^t /(cos t))dt−∫_0 ^( t) e^t (−(1/(cos^2 t))d(cost))= =((sint)/(cos^2 t))e^t −∫_0 ^( t) (e^t /(cos t))dt−∫_0 ^( t) e^t d((1/(cos t)))= =((sint)/(cos^2 t))e^t −∫_0 ^( t) (e^t /(cos t))dt−{[(e^t /(cos t))]_0 ^t −∫_0 ^( t) (e^t /(cos t))dt}= =((sint)/(cos^2 t))e^t −(e^t /(cos t))+1= =(e^t /(cos t))(tan t − 1)+1= =(x−1)(√(1+x^2 ))e^(arctan(x)) +1 ⇒(x−1)(√(1+x^2 ))e^(arctan(x)) +1=1 ⇒x=1](https://www.tinkutara.com/question/Q173209.png)
Commented by peter frank last updated on 08/Jul/22

Commented by aleks041103 last updated on 08/Jul/22

Commented by Shrinava last updated on 08/Jul/22