Question Number 179449 by Shrinava last updated on 29/Oct/22
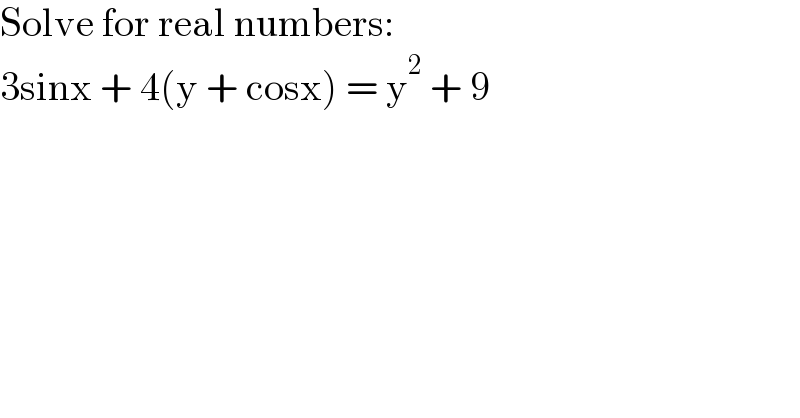
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{3sinx}\:+\:\mathrm{4}\left(\mathrm{y}\:+\:\mathrm{cosx}\right)\:=\:\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{9} \\ $$
Answered by mr W last updated on 29/Oct/22
![3 sin x+4 cos x−5=y^2 −4y+4 5[sin (x+α)−1]=(y−2)^2 since sin (x+α)≤1, LHS ≤0. but RHS≥0, therefore LHS=RHS=0 ⇒sin (x+α)=1 ⇒x=2kπ+(π/2)−tan^(−1) (4/3) ⇒y=2](https://www.tinkutara.com/question/Q179457.png)
$$\mathrm{3}\:\mathrm{sin}\:{x}+\mathrm{4}\:\mathrm{cos}\:{x}−\mathrm{5}={y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4} \\ $$$$\mathrm{5}\left[\mathrm{sin}\:\left({x}+\alpha\right)−\mathrm{1}\right]=\left({y}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${since}\:\mathrm{sin}\:\left({x}+\alpha\right)\leqslant\mathrm{1},\:{LHS}\:\leqslant\mathrm{0}. \\ $$$${but}\:{RHS}\geqslant\mathrm{0},\:{therefore} \\ $$$${LHS}={RHS}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\left({x}+\alpha\right)=\mathrm{1}\:\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow{y}=\mathrm{2} \\ $$
Commented by Shrinava last updated on 01/Nov/22

$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
Answered by manxsol last updated on 29/Oct/22

$$\mathrm{3}{sinx}+\mathrm{4}{cosx}={y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9} \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}{sinx}+\frac{\mathrm{4}}{\mathrm{5}}{cosx}=\frac{{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}}{\mathrm{5}} \\ $$$${sin}\left({x}+\theta\right)=\frac{{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}}{\mathrm{5}}\: \\ $$$$\theta={arsen}\left(\mathrm{3}/\mathrm{5}\right) \\ $$$$−\mathrm{1}\leqslant\frac{{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}}{\mathrm{5}}\leqslant\mathrm{1} \\ $$$$−\mathrm{5}\leqslant{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}\:\hat {\Lambda}\:{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}\leqslant\mathrm{5} \\ $$$$\mathrm{0}\leqslant{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{14}\:\:\:\Delta=\mathrm{16}−\mathrm{56} \\ $$$$\:\:\:\:\:\Delta<\mathrm{0}\Rightarrow{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{14}\:\rangle\mathrm{0}\:\:\:\forall{y}> \\ $$$${y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{9}\leqslant\mathrm{5} \\ $$$${y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4}\leqslant\mathrm{0} \\ $$$$\left({y}−\mathrm{2}\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$$${solution}\:{y}=\mathrm{2}\:\:\: \\ $$$${sin}\left({x}+\theta\right)=\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{2}\right)+\mathrm{9}}{\mathrm{5}}=\mathrm{1} \\ $$$${x}+\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$${x}=\left(\frac{\pi}{\mathrm{2}}−{arcsin}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)\right)+\mathrm{2}{k}\pi \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Shrinava last updated on 01/Nov/22

$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
